(2х-5)(3х+4)=6x^2+8x-15x-20=6x^2-7x-20
(х-3у)(2у-5х)=2xy-5x^2-6y^2+15xy=-5x^2+17xy-6y^2
а(а-5)-(а-2)(а-3)=a^2-5a-a^2+3a+2a-6=-6
(2b+1)(4b^2-2b+1)=8b^3-1
х^3+2х^2+х+2=x(x^2+1)+2(x^2+1)=(x+2)(x^2+1)
4х-4у+ху-у^2=4(x-y)+y(x-y)=(4+y)(x-y)
№3
2х^2(4х^2-3)(3+4х^2)=32х^6-18х^2
(8x^4-6x^2)(3+4x^2)=32x^6-18x^2
24x^4+32x^6-18x^2-24x^2=32x^6-18x^2 24x^4-24x^4=0
32x^6-18x^2=32x^6-18x^2
№4
а^2-bc+ab-ac=a(a-c)+b(a-c)=(a+b)(a-c)
3а+ab^2-а^2b-3b=3(a-b)-ab(a-b)=(3-ab)(a-b)
№5
x-2=y+1 x=y+3
(x-2)(y+1)=xy-4
(y+1)(y+1)=y^2+3y-4
y^2+2y-y^2-3y=-5 y^2-y^2=0
-y=-5
y=5
x=y+3
x=5+3
x=8
проверка
y+1=5+1=6
x-2=8-2=6
6*6=36 5*8=40
40-36=4
сторона квадрата равно 6
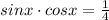
![[-\pi;\pi]](/tpl/images/0144/2399/fdb8f.png)
Чтобы решить это уравнение, нужно привести к одной функции (т.е. чтобы либо только cos, либо только sin)
Вспоминаем формулу синуса двойного угла: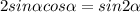 
Она бы нам подошла, если бы слева перед синусом и косинусом стояла двойка. Так как ее нет, мы подгоняем:
Эти уравнения совершенно равнозначны: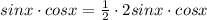 
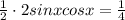
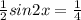
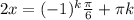
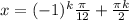
Это общее уравнение, а нам нужны корни на заданном промежутке. Промежуток ![[-\pi; \pi]](/tpl/images/0144/2399/0c866.png)
для удобства можем представить как ![[\frac{-12 \pi}{12}; \frac{12 \pi}{12}]](/tpl/images/0144/2399/c0238.png)
. Так удобнее для сравнения. Делаем выборку, подставляя вместо k разные целые числа: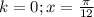
- этот корень принадлежит данному промежутку
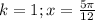-принадлежит
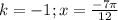- принадлежит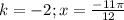
Получилось что 4 корня принадлежат.
ответ: 4
3дес тыс 7ед тыс 6 сот 8 ед
2сот тыс 4дес тыс 2ед тыс 6дес 4ед
3сот тыс 7дес тыс 8сот 6дес
5сот тыс 6дес тыс 3ед тыс 5ед
1сот тыс 6ед тыс 8ед
1сот тыс 4дес тыс 5сот 9ед
2сот тыс 5ед тыс 3сот 7дес