Возьмем приближенно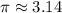 
Рассмотрим число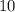 
. На числовой окружности этому числу соответствует та же точка, что и числу 
:
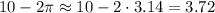
Зная, что 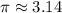и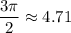 
, получаем, что число 
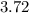располагается в 3 четверти. Значит, можно сказать о знаках тригонометрических функций: косинус и синус - отрицательный, тангенс и котангенс - положительный. Остается сравнить между собой данные две пары.
Заметим, что число 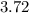располагается ближе к числу 
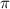, так как 
.
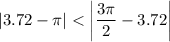Зарисуем схематично число в 3 четверти, расположенное ближе к числу 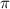. По рисунку определим, что косинус такого числа (координата х) меньше синуса (координата y):
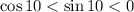
Рассмотрим тангенс. Так как тангенс положительный, то заменим отношение синуса к косинусу отношением их модулей:
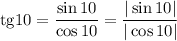
Зная, что 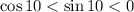, получим, что 
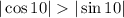, соответственно дробь 
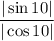правильная, значит 
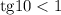. Тогда, так как котангенс есть величина, обратная тангенсу, то 
.
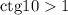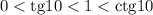
Итоговая цепочка: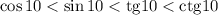 
\[x_0=-\frac{b}{2a}=-\frac{0}{2\cdot \left(-1\right)}=0\]
Подставим найденную абсциссу в уравнение функции и найдем ее ординату:
\[y_0=-0^2+4=4\]
Итак, вершиной параболы будет точка (0; 4).
Далее нужно найти точки, которые принадлежат графику параболы. Сделать это легко. Берем несколько произвольных значений переменной х и вычисляем для них значение переменной у. Полученные пары чисел будут координатами искомых точек.
х = 1: y\left(1\right)=-1^2+4=3 —точка с координатами (1; 3).
х = 2: y\left(2\right)=-2^2+4=0 —точка с координатами (2; 0).
х = —1: y\left(-1\right)=-{\left(-1\right)}^2+4=3 —точка с координатами (—1; 3).
х = —2: y\left(-2\right)=-{\left(-2\right)}^2+4=0 —точка с координатами (—2; 0). Нанесем найденные точки на координатную плоскость и начертим график функции y = —x^2 + 4
(Рисуешь точку и проводишь линии в право ,влево ,вперед и назад.Расставляешь числа ,рисуешь дугу с самого низа до верха по второе число и спускаешься вниз)Думаю понятно объяснила.
Содержит 7 букв, 3 слога, 7 звуков, транскрипция слова - [пр'ииски], Ударение ставится на 1-й слог, на букву и — при́иск.
п — [п] — согласный, парный глухой, парный твёрдый
р — [р'] — согласный, непарный звонкий, сонорный, парный мягкий
и — [и] — гласный
и — [и] — гласный
с — [с] — согласный, парный глухой, парный твёрдый
к — [к] — согласный, парный глухой, парный твёрдый
и — [и] — гласный
Состав слова «прииск»: приставка [при] + корень [иск] + нулевое окончание []
Основа(ы) слова: прииск
образования слова: префиксальный (приставочный)