у = x² - 2x - 8
y = (x² - 2x + 1) - 1 - 8
y = (x - 1)² - 9
График функции - квадратичная парабола, ветви направлены вверх.
Координаты вершины из уравнения y = (x - 1)² - 9
x₀ = 1; y₀ = -9.
Нули функции
x² - 2x - 8 = 0 ⇔ (x - 4)(x + 2) = 0
1) x - 4 = 0; x₁ = 4;
2) x + 2 = 0; x₂ = -2
Точка пересечения с осью OY для построения графика
x = 0; y = x² - 2x - 8 = 0² - 2*0 - 8 = -8
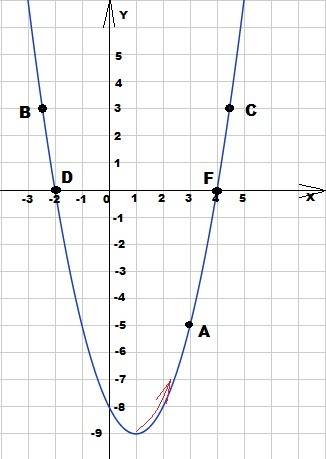
График в приложении.
а) x = 3; y = 3² - 2*3 - 8 = 9 - 6 - 8 = -5
A (3; -5)
б) y = 3;
x² - 2x - 8 = 3 ⇔ x² - 2x - 11 = 0
D/4 = (b/2)² - ac = 1 + 11 = 12
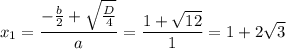 ≈ 4,5
≈ 4,5
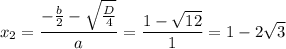 ≈ -2,5
≈ -2,5
B (-2,5; 3); C(4,5; 3)
в) Нули функции x₁ = 4; x₂ = -2
Точки D (-2; 0); F(4; 0)
Промежутки знакопостоянства функции
y > 0 при x ∈ (-∞; -2) ∪ (4; +∞)
y < 0 при x ∈ (-2; 4)
г) Функция возрастает при x ∈ [1; +∞)
============================
Графики у = 1/3 x²; у = 6x - 15
Для поиска точки пересечения нужно уравнять формулы по y
1/3 x² = 6x - 15 | * 3
x² = 18x - 45 ⇔ x² - 18x + 45 = 0
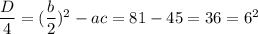
Дискриминант положительный, значит, графики имеют 2 точки пересечения.
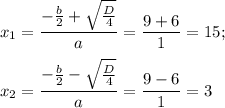
1) x₁ = 15; y₁ = 6*15 - 15 = 5*15 = 75
2) x₂ = 3; y₂ = 6*3 - 15 = 18 - 15 = 3
ответ: точки пересечения графиков (15; 75); (3; 3)
1)
a^2+8a+16
2)
9y^2-6y*c+c^2
3)
4a^2+10a-10a-25=4a^2-25
4)
x^4-x^2*y+x^2*y-y^2=x^4-y^2
Разложить на множители:
1)
0,36-с^2= (0,6)^2-(sqrt(c))^2=(0,6-sqrt(c))*(0,6+sqrt(c))
2)
a^2+10a+25=(5+a)^2
Выполнить действия:
1)
(a+b)^2-(a-b)^2= a^2+2a*b+b^2-a^2+2a*b-b^2=4a*b
2)
(x^2-y^3)^2= x^4-2x^2*y^3+y^6
Решить уравнение:
16y^2-49=0
y^2=49/16
y=7/4
ответ: y=7/4