Разложим оба числа на простые множители:
1960 = 980*2 = 490*2*2 = 275*2*2*2 = 49*5*2*2*2 = 7*7*5*2*2*2 = 7² * 5 * 2³
588 = 294*2 = 147*2*2 = 49*3*2*2 = 7*7*3*2*2 = 7² * 3 * 2²
После расложения, получаем:
1960 = 7² * 5¹ * 3⁰ * 2³
588 = 7² * 5⁰ * 3¹ * 2²
НОД(a, b) равен произведению множителей, которые входят в разложение на простые множители обоих чисел. То есть надо брать наименьшие степени из этих разложений.
7² входит и в то, и в другое число. 5⁰ < 5¹, поэтому для НОД мы возьмём наименьшую степень, то есть 5⁰. Аналогично, рассматривая тройки, возьмём 3⁰, а сравнивая двойки, возьмём 2²
НОД (1960, 588) = 7² * 5⁰ * 3⁰ * 2² = 49 * 4 = 196
НОК(a, b) равно произведению множителей, которые входят в хотя бы одно разложение чисел на простые множители. То есть надо брать наибольшие степени из этих разложений.
7² входит и в то, и в другое число. 5⁰ < 5¹, поэтому для НОК мы возьмём наибольшую степень, то есть 5¹. Аналогично, рассматривая тройки, возьмём 3¹, а сравнивая двойки, возьмём 2³.
НОК(1960, 588) = 7² * 5¹ * 3¹ * 2³ = 49 * 5 * 3 * 8 = 5880
Двузначное число, где а десятков и b единиц представим в виде 10a+b (это разложение числа по разрядам). Далее записываем условие задачи: 1) первое предложение
(10a+b):(a+b)=7(ост.3)
10a+b=7(a+b)+3
10a+b=7a+7b+3
3a-6b=3
a-2b=1 - это первое уравнение системы.
2) читаем второе предложение задачи
При перестановке цифр данного двузначного числа получим число 10b+a. Известно, что оно на 36 меньше, чем число 10a+b. Запишем это: 10a+b-36=10b+a
9a-9b=36 |:9
a-b=4 - это второе уравнение системы
Решаем систему:
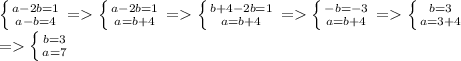
Итак, искомое двузначное число равно 73.
1) (3x+5)^2- (2x+5)^2= 0
(3x+5-2x-5) (3x+5+2x+5) =0
x (5x+10)= 0
x=0 или 5х+10 =0
5(х+ 2) =0
х=-2
ответ: 0, -22) (2x-1)^2-(x-2)^2=0 (2х-1-х+2) (2х-1+х-2) = 0 (х+1) (3х-3) =0 х+1= 0 или 3х-3=0 х=-1 2(х-1) =0 х=1ответ: -1, 1 1)9x^2+30x+25-(4x^2+20x+25)=5x^2+10x;5x^2+10x=0x(5x+10)=0x1=0 или 5x=-10 x=-22)4x^2-4x+1-(x^2-4x+4)=3x^2-3;3x^2-3=0;x^2=1x1=1 или х2=-1