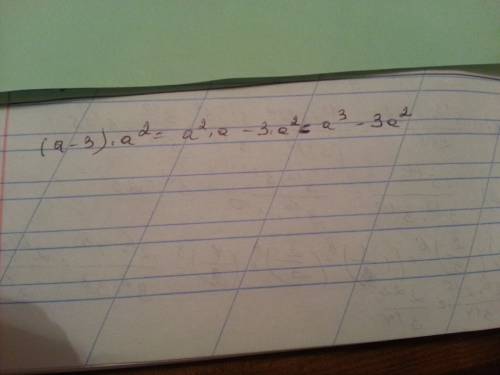
a) корень из 18 надо представить как корень из 9*2, тогда корень из 9=3, и под корнем останется 2
я заменю слово корень значком V, чтобы писать покороче, ладно? То есть V18=3V2, отсюда
1,4<V2<1,5
3*1,4<3V2<3*1,5
4,2<V18<4,5 т.к. 2,2<V5<2,3 то из первого неравенства вычтем второе и получим
2<V18-V5<2,2
б) 1,4<V2<1,5 V10=V2*V5, а 2,2<V5<2,3, значит выражение V2+V5=V2(1+V5) найдем границы выражения 1+V5 1+2,2<1+V5<1+2,3 это будет 3,2<(1+V5)<3,3 теперь перемножим все части первого и последнего неравенств
1,4*3,2<V2*(1+V5)<1,5*3,3 4,48<V2+V10<4,95
ответ: 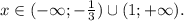
Объяснение:
-3x² + 2x +1 < 0;
3x² - 2x - 1 > 0;
Дискриминант равен 2²+4*1*3 = 4+12 = 16.
Корни трехчлена равны 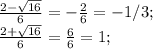
Значит 3x² - 2x - 1 = (3x+1)(x-1) > 0;
Рассмотрим значение выражения на каждом из интервалов: (-∞; -1/3); (-1/3; 1); (1; +∞). На первом из них 3х+1 < 0 и х-1 < 0. Значит произведение больше 0. На втором 3х+1 > 0 и х-1 < 0. Значит их произведение меньше 0. На третьем 3х+1 > 0 и х-1 > 0. Значит их произведение больше 0. Подходит только интервал (-∞; -1/3) и (1; +∞)
ответ: a^3 - 3*a^2.