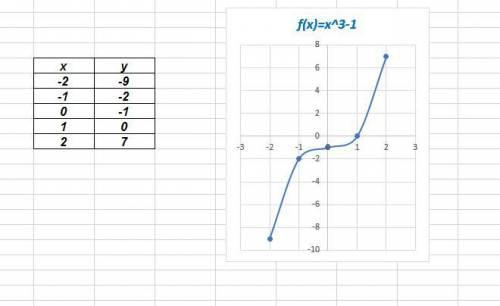
f(x)=x^3-1
График - кубическая парабола
График расположен в I, III, IV четвертях координатной плоскости
Пересечение с осью Х - точка (1;0)
Пересечение с осью У точка (0;-1)
Область определения: D=x∈(-∞;+∞) множество действительных чисел
Область значений: Е=у∈(-∞;+∞) множество действительных чисел
Непрерывна на всей числовой прямой
Нули функции: (1;0)
Промежутки знакопостоянства: y>0 при x∈(1;+∞), y<0 при x∈(-∞;1)
Возрaстает по всей числовой прямой:
х₁=-2, у₁=2; х₂=2, у₂=7 => x₁<x₂→y₁<y₂
График выпуклый на промежутке (-∞;0)), вогнутый - (0;+∞)
Функция не четная и не нечетная:
Если х=1, то x^3-1≠-x^3-1
0≠-2
х^3-1≠(-1)*(-х^3-1)
0≠2
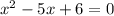
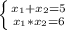
Значит, если к произведению прибавить любое число делящееся на 2 или на 3, мы никак не сможем получить простое (сумма тоже будет делиться на 2 или на 3)
Значит наименьший кандидат для n - это число 5.
И действительно, такой пример есть
2*3*4+5 = 29 - простое.