для меня это самое понятное... надеюсь
Объяснение:
Предположим, что нам нужно составить квадратное уравнение, корнями которого были бы числа x1 и x2. Очевидно, что в качестве искомого уравнения можно выбрать уравнение
a(х — x1)(х — x2) = 0, (1)
где а — любое отличное от нуля действительное число. С другой стороны, каждое квадратное уравнение с корнями x1 и x2 можно записать в виде (1).
Таким образом, формула (1) полностью решает поставленную выше задачу. Из всех квадратных уравнений корни x1 и x2 имеют уравнения вида (1) и только, они.
Пример. Составить квадратное уравнение, корни которого равны 1 и — 2.
ответ. Корни 1 и —2 имеют все квадратные уравнения вида
а(х — 1)(х + 2) = 0,
или
ах2 + ах — 2а = 0,
где а — любое отличное от нуля действительное число. Например, при а = 1 получается уравнение
х2 + х — 2 = 0.
Объяснение:
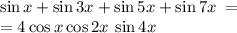
Проведем доказательство тождества следующим образом:
- проведем равносильные преобразования левой части доказываемого тождества;
- если в итоге преобразований левая часть примет ту же форму что и правая часть - тождество доказано.
Итак - левая часть:
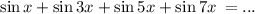
Сгруппируем следующим образом:
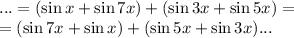
Воспользуемся формулой суммы синусов:
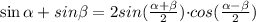
Поочередно сложим группы внутри скобок:
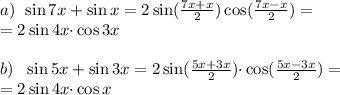
Тогда вся левая часть примет вид:
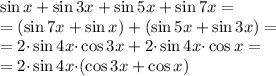
для преобразования суммы косинусов в скобках воспользуемся такой формулой:
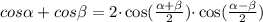
Выражение примет вид:
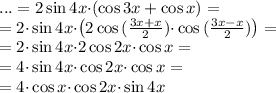
В результате преобразований левая часть приняла тот же вид что и правая.
Тождество доказано.
А) 8=2³
Б) 125=5³
В) 64k³=(4k)³
Г) x³n6=(xn²)³
Д) 27b9=(3b³)³
Е) a3m6=(am²)³
Ж) 0,001f6=(0,1f²)³
З) (1/64)d24=(1/4d^8)³
2. Представьте выражение в виде суммы кубов:
А) у3+8=y³+2³
Б) 27+a3=3³+a³
В) 1+m3=1³+m³
Г) x9+64=(x³)³+4³
Д) n6+8t3=(n²)³+(2t)³
Е) a9+125d3=(a³)³+(5d)³
Ж) 0,001f6+c12=(0,1f²)³+(c⁴)³
З) 64d24+s12=(4d^8)³+(s⁴)³
3. Разложите многочлен на множители:
А) у3+n3=(y+ n)(y²-yn+n²)
Б) 1+a3=(1+a)(1-a+a²)
В) s3+m3=(s+m)(s²-sm+m²)
Г) x9+t6=(x³+y²)(x^6-x³y²+y⁴)
Д) n6+h6=(n²+h²)(n⁴-n²h²+h⁴)
Е) a6+d15=(a²+d5)(a⁴-a²d5+d10)
Ж) 27f3+c3=(3f+c)(9f²-3fc+c²)
З) 64d3+v3=(4d+v)(16d²-4dv+v²)
И) 8z6+y12=(2z²+y⁴)(4z⁴-2z²y⁴+y8)
К) q3+125r15=(q+5r5)(q²-5qr5+25r10)
4.Запишите выражение в виде многочлена, используя формулу суммы кубов двух чисел:
А) (m+n)(m2-mn+n2)=m³+n³
Б) (a+1)(a2-a+1)=a³+1
В) (p2-4p+16)(p+4)=p6+64
Г) (p+q)(p2-pq+q2)=p³+q³
Д) (2+x)(4-2x+x2)=8+x³
Е) (25-5m+m2)(5+m)=125+m³