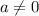2,периметр прямоугольника равен 20 см. найдите его стороны, если известно, что площадь прямоугольника равна 24 см2 3.в уравнении х 2 + pх – 18 = 0 один из его корней равен -9. найдите другой корень и коэффициент p.

👇

Ответ:

drart77

10.01.2022

Площадь равна : Х*у=24
а периметр равен: 2х+2у=20
решаем систему 1)х=24/у
2*24/у+2у=20
2)решаем уравнение и находим у
48/у+2у=20
2у^2-20у+48=0
у^2-10у+24=0
дискр=100-4*24=100-96=4
у=4;6
значит х=6;4
значит стороны равняется 6 и 4;или 4 или 6
2 номер
-9^2-9р-18=0;отсюда р=63/9=7
находим х2
х^2+7х-18=0
дискр=121
х2=1

4,7(16 оценок)

Открыть все ответы

Ответ:

Bow9718

10.01.2022

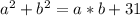Пусть десятки - это а, единицы - это b. Заметим, что $a\neq 0$ . Иначе уже число не двузначное :)). a=1,2,3,4,5,6,7,8,9 - это все возможные числа. b=0,1,2,3,4,5,6,7,8,9. Сумма квадратов цифр равна a^2+b^2=a*b+31

- это по условию задачи.

a^2+b^2-ab=31

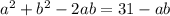
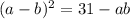
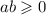Заметим, что у нас должен получиться слева квадрат некоего числа. Значит и справа должен быть квадрат. Так как $ab\geqslant 0$ , то правая часть меньше или равна 31. Значит надо найти квадраты чисел меньших 31, но больше 0. Задача вполне выполнимая. В порядке убывания 25, 16, 9, 4,1. 0 - на всякий случай.

При 25, получаем 31-ab=25, Из этого следует, что ab=6. Причем оба этих числа положительны.
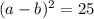С другой стороны (a-b)^2=25

. При а=1 и b=6, а также, наоборот, а=6, b=1 получаем, что квадрат разности выполняется. При а=3 и b=2, и наоборот, квадрат разности не выполняется. То есть подходят только пары а=6, b=1 и а=1 и b=6.

При 16, получаем 31-ab=16. Из этого следует, что ab=15. Получается пара чисел а=5, b=3, или наоборот. Но вот квадрат разности не даст желаемых 16. Другие пары здесь невозможны. 15 и 1 не подойдут.

При 9, получаем 31-ab=9. ab=22. Тут снова не выходит пара чисел. Так как 22=2*11. Эти числа не могут быть а и b. 22=1*22 - тоже не нужный вариант.

При 4, получаем 31-ab=4. ab=27. Тут получается пара чисел 9 и 3. Но вот квадрат их разности будет равен 36. А это не дает 4.

При 1, получаем ab=30. Пара допустимая будет a=5, b=6 или a=6, b=5. Здесь квадрат разности будет равен 1. То есть (a-b)^2=1

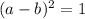. То есть получаем числа 65 и 56. Остальные пары, вроде 2 и 15 недопустимы.

Таким образом, перебрали все возможные варианты и пришли к 4 числам 16, 61, 56, 65.

Теперь вычислим их сумму: 16+61+65+56=77+121=198.

ответ: 198 - это сумма нужных нам двузначных чисел.

4,5(72 оценок)

Ответ:

Tinusya

10.01.2022

,Решение:
Зная первоначальную скорость, обозначенную за х, найдём время за которое мотоциклист км: 36/х (час), тогда 46 км мотоциклист пойдёт за 46/(х+10)
И так как он это расстояние за 2 часа, составим уравнение вида:
36/х+46/(х+10=2
Приведём данное уравнение к общему знаменателю х*(х+10) и получим:
36х+360+46х=2х^2+20х
2x^2+20x-36x-46x-360=0
2x^2-62x-360=0 Можно данное уравнение привести к упрощённому виду разделив его на2
x^2-31-180=0
x1,2=31/2+-sqrt(961/4+720/4)=31/2+-sqrt(1681/4)=31/2+-41/2
x1=31/2+41/2=36
x2=31/2-41/2=-10/2=-5 (не соответствует условию задачи)

ответ: Начальная скорость мотоциклиста 36км/час

4,7(77 оценок)

Это интересно:

Финансы-и-бизнес

08.08.2021

Как заключить брачный договор в Таиланде: советы для тех, кто собирается расписываться...

Хобби-и-рукоделие

24.04.2020

Как сделать бумажный вертолет...

Кулинария-и-гостеприимство

18.08.2021

Сделай свой день еще сладким: как сделать букет из конфет...

Компьютеры-и-электроника