Алгебра: Решите уравнение: 1) x² + 12x + 36 = 0 2) 25x² - 30x + 9 = 0 3) (x + 3)² + (4 - x)² = 2(x - 4)(x + 3)

1) Новый общий знаменатель для двух дробей это y в максимальной присутствующей степени, т.е. y^{4}. Тогда дополнительным множителем к первой дроби будет единица, а ко второй дроби y^{3}. Получается rac{2x}{y^{4}} и rac{3x^{3}}{y^{4}}. 2) Дополнительный множитель к первой дроби будет y, а ко второй a^{5}. Получается rac{2by}{ya^{5}} и rac{6a^{5}}{ya^{5}}. 3) Новый общий знаменатель для двух дробей будет это 6x^{2}y^{2}. Тогда дополнительный множитель к первой дроби будет 2x, а ко второй...

Решите уравнение: 1) x² + 12x + 36 = 0 2) 25x² - 30x + 9 = 0 3) (x + 3)² + (4 - x)² = 2(x - 4)(x + 3)

👇

Увидеть ответ

Ответ:

nikolay2045

04.05.2020

1) x² + 12x + 36 = 0
(х+6)²=0
х+6=0
х=-6
ответ: -6

2) 25x² - 30x + 9 = 0
(5х-3)²=0
5х-3=0
5х=3
х=3/5
ответ: 3/5

3) (x + 3)² + (4 - x)² = 2(x - 4)(x + 3)
(x + 3)² + (4 - x)² - 2(x - 4)(x + 3)=0
(x + 3)² + (х - 4)² - 2(x - 4)(x + 3)=0
((х+3)-(х-4)) ²=0
(х+3-х+4)²=0
7²=0 - корней нет
ответ: корней нет

4,5(11 оценок)

Открыть все ответы

Ответ:

alicemuhametp0aof9

04.05.2020

В обеих точках функция непрерывна

Объяснение:

Для ответа на данный вопрос найдём пределы слева и справа от указанных точек, если пределы совпадают, то функция в данной точке непрерывна, если не совпадают, то функция имеет разрыв первого рода, а если хотя бы один из пределов равен бесконечности или не существует, то в данной точке функция имеет разрыв второго рода.

для x = 0

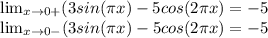
$\lim_{x \to 0+} (3sin(\pi x) - 5cos(2\pi x) = -5\\ \lim_{x \to 0-} (3sin(\pi x) - 5cos(2\pi x) = -5$

Как видим, пределы слева и справа совпадают, следовательно f(0) непрерывна

для x = 1

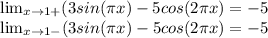
$\lim_{x \to 1+} (3sin(\pi x) - 5cos(2\pi x) = -5\\ \lim_{x \to 1-} (3sin(\pi x) - 5cos(2\pi x) = -5$

Снова видим, что пределы совпадают, следовательно и при f(1) функция непрерывна.

4,4(8 оценок)

Ответ:

123Настенька

04.05.2020

1) Новый общий знаменатель для двух дробей это y в максимальной присутствующей степени, т.е.  y^{4}. Тогда дополнительным множителем к первой дроби будет единица, а ко второй дроби  y^{3}.
Получается \frac{2x}{y^{4}} и \frac{3x^{3}}{y^{4}}.
2) Дополнительный множитель к первой дроби будет y, а ко второй a^{5}. Получается  \frac{2by}{ya^{5}} и \frac{6a^{5}}{ya^{5}}.
3) Новый общий знаменатель для двух дробей будет это 6x^{2}y^{2}.
Тогда дополнительный множитель к первой дроби будет 2x, а ко второй y. Получается  \frac{7y}{6x^{2}y^{2}} и \frac{4x}{6x^{2}y^{2}}.
4) Новым общим знаменателем для двух дробей будет 7x(x+5). Тогда дополнительным множителем к первой дроби будет 7x, а ко второй (x+5). Получается \frac{28x}{7x(x+5)} и \frac{3x+15}{7x(x+5)}.
5) Т.к. новый общий знаменатель должен включать в себя все множители из обоих дробей, то он будет равен (3x-3y)(4x+4y). Из каждой скобки можно вынести общий множитель, перемножить их, а скобки свернуть по формуле "разность квадратов":
(3x-3y)(4x+4y)=3(x-y)4(x+y)=12(x^{2}-y^{2}). ответ и будет являться новым общим знаменателем.
Дополнительный множитель к первой дроби будет (3x-3y), а ко второй (4x+4y). Получается \frac{8x^{2}+8xy}{12(x^{2}-y^{2})} и \frac{9xy-9y^{2}}{12(x^{2}-y^{2})}.
6) Из знаменателя первой дроби вынесем общий множитель:
2a+2=2(a+1). Таким образом новый общий знаменатель будет равен 2(a+1). Дополнительный множитель к первой дроби будет 1, а ко второй 2. Получается \frac{a}{2(a+1)} и \frac{6}{2(a+1)}.

4,7(58 оценок)

Это интересно:

Компьютеры-и-электроника

26.03.2023

Как изменить проверочный номер для кода безопасности iCloud на iPhone...

Семейная-жизнь

28.05.2021

Как помочь родителям, которые похоронили своего ребенка: советы и рекомендации...

Здоровье

03.04.2021

Как вылечить прищемленный палец: лечение дома и медицинские советы...

Дом-и-сад