Теорема (о сумме углов выпуклого многоугольника)
Сумма внутренних углов выпуклого многоугольника равна 180º(n-2). (n — количество сторон многоугольника).
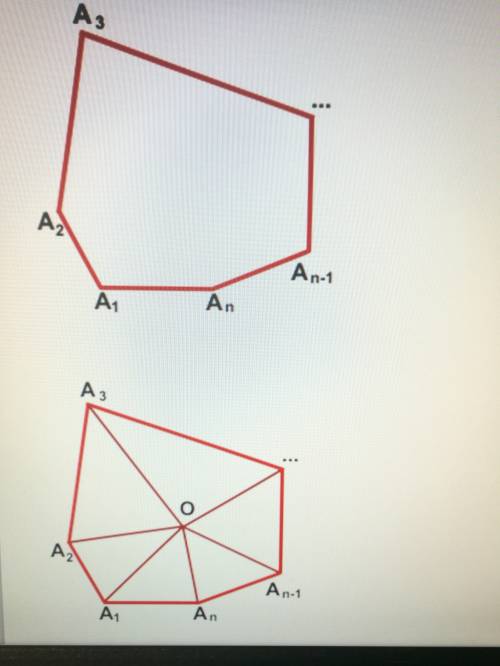
(смотри верхний рисунок)
— выпуклый n -угольник.
Обозначим внутри многоугольника произвольную точку O.
Соединим точку O с вершинами многоугольника.
(смотри нижний рисунок)
Получили n треугольников.
Сумма внутренних углов многоугольника равна сумме углов всех треугольников без углов при вершине O.
То есть в данном случае у нас 6-угольник, имеем 6 треугольников, сумма углов которых 6*180 и минус 2*180 – сумма углов при вершине. Получается 180*(6 – 2) = 720 гр.
Так как сумма углов при вершине O составляет 360º, то сумма углов многоугольника равна сумме углов n треугольников минус 360º.
= - x^3 - 6x^2 - 12x - 8 + x^3 - 6x^2 + 12x - 8 =
= - 12x^2 - 16 =
= - 4(3x^2 + 4)