1.
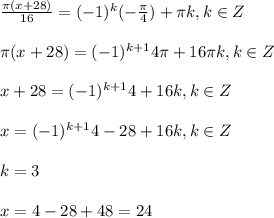
наименьший положительный х=24
2.
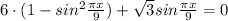
Квадратное уравнение относительно синуса
6t²-√3·t-6=0
D=3+144=147
√D=√(3·49)=7·√3
t₁=-√3/2; t₂=2√3/3 > 1
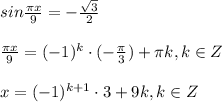
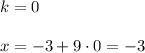
наибольший отрицательный
4.
Так как
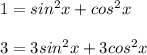
уравнение имеет вид:
2cos²x+6√3sinx·cosx+3sin²x+3cos²x=0
3sin²x+6√3sinx·cosx+5cos²x=0
Это однородное тригонометрическое уравнение.
Делим на cos²x≠0
3tg²x+6√3tgx+5=0
D=(6√3)²-4·3·5=108-60=48
√D=4√3
tgx=-5√3/3 или tgx=-√3/3
x=arctg(-5√3/3) +πk, k∈Z или x=arctg(-√3/3)+πn, n∈Z
Функция y=arctgx - монотонно возрастающая на (-∞;+∞)
-(5√3/3) < (-√3/3)⇒arctg(-5√3/3) < arctg(-√3/3)
Наибольший отрицательный
n=0
x=atctg(-√3/3)=-30°
x + y + z = 1 (1)
x^2 + y^2 + z^2 = 4 (2)
x^3 + y^3 + z^3 = 6 (3)
x^4 + y^4 + z^4 = ?
не совсем все просто
надо очень хорошо знать квадраты и кубы многочленов
Итак
(x + y)^2 = x^2 + 2xy + y^2
(x + y)^3 = x^3 + 3x^2y + 3xy^2 + y^3
(x + y + z)^2 = (x + y)^2 + 2(x + y)z + z^2 = x^2 + y^2 + z^2 + 2(xy + yz + xz) (4) аналогично и квадраты
(x^2 + y^2 + z^2)^2 = (x^2 + y^2)^2 + 2(x^2 + y^2)z^2 + z^4 = x^4 + y^4 + z^4 + 2(x^2y^2 + y^2z^2 + x^2z^2) (5)
рассмотрим 4
x^2 + y^2 + z^2 + 2(xy + yz + xz) = 1
2(xy + yz + xz) = 1 - 4
xy + yz + xz = - 3/2
(x + y + z)^3 = (x + y)^3 + 3(x + y)^2z + 3(x + y)z^2 + z^3 = x^3 + 3x^2y + 3xy^2 + y^3 + 3x^2z + 6xyz + 3y^2z + 3xz^2 + 3yz^2 + z^3
6xyz = (x + y + z)^3 - 3(x + y + z)(x^2 + y^2 + z^2) + 2(x^3 + y^3+z^3)
6xyz = 1 - 3*1*4 + 2*6 = 1 - 12 + 12 = 1
xyz = 1/6
и наконец
(x^2 + y^2 + z^2)^2 = (x^2 + y^2)^2 + 2(x^2 + y^2)z^2 + z^4 = x^4 + y^4 + z^4 + 2(x^2y^2 + y^2z^2 + x^2z^2) (5)
x^4 + y^4 + z^4 = (x^2 + y^2 + z^2)^2 - 2(x^2y^2 + y^2z^2 + x^2z^2) = (x^2 + y^2 + z^2)^2 - 2((xy + yz + xz)^2 - 2xyz(x+ y + z))
получили окончательную формулу
x^4 + y^4 + z^4 = (x^2 + y^2 + z^2)^2 - 2((xy + yz + xz)^2 - 2xyz(x+ y + z))
x^4 + y^4 + z^4 = 4^2 - 2((-3/2)^2 - 2*1/6*1) = 16 - 2(9/4 - 1/3) = 16 - 2(27 - 4)/12 = 16 - 23/6 = 16 - 3 5/6 = 12 1/6 = 73/6
ответ 73/6
проверьте - вроде правильно
ответ: 37