Периметр любой фигуры равен сумме длинн всех сторон, т.к у квадрата они равны и их 4, то его сторона равна 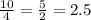
У прямоугольника протиоположные стороны равны. Его стороны могут быть1) 2 и 6; 2) 1 и 4, 3) 2 и 3.
Площать двадрата: 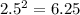
Площать прямоугольника: 1)2*6=12 2) 1*4=4 3) 2*3=6
1) Площать квадрата 6.25, прямоугольника 12. Площать прямоугольника больше на 5.75см
2) Площать квадрата 6.25, прямоугольника 4. Площать квадрата больше на 2.25см
3) Площать квадрата 6.25, прямоугольника 6. Площать прямоугольника больше на 0.25см
10/4=2.5 см. Одна сторона квадрата.
(1+1)+(4+4)=10 т.е две стороны по 1 и две стороны по 4 прямоугольник
(2+2)+(3+3)=10 т.е две стороны по 2 и две стороны по 3 прямоугольник
(3,5+3,5)+(1,5+1,5) = 10 т.е две стороны по 3,5 и две стороны по 1,5 прямоугольник
(1*4) меньше чем (2,5*2,5) = 4 меньше чем 13,75 т.е прямоугольник меньше площадью чем квадрат.
(2*3) меньше чем (2,5*2,5) = 6 меньше чем 13,75 т.е прямоугольник меньше площадью чем квадрат
(3,5*2,5) меньше чем (2,5*2,5) = 8,75 меньше чем 13,75 т.е прямоугольник меньше площадью чем квадрат
Аналогично получаем уравнение прямой BC y = –3x/4 + 17/4, которая пересекает Ox в x = 17/3, назовём эту точку N.
Тогда MN = 17/3 – 3/2 = 25/6 как основание прямоугольного треугольника BMN (угол B — прямой). Высота данного треугольника равна абсциссе точки B — 2. Таким образом, площадь треугольника равна 0.5(2)(25/6) = 25/6.
Найдём расстояние (а оно же и сторона квадрата) между точками A и B: AB = √(9 + 16) = 5, здесь же найдём площадь всего квадрата: 5² = 25. Тогда площадь пятиугольника MNCDA равна 25 – 25/6 = 125/6.
Наконец, найдём искомое отношение площадей треугольника BMN к пятиугольнику MNCDA: 25/6 : 125/6 = 25 : 125 = 1 : 5.
ответ: 1 : 5.