Так как в уравнении есть квадратные корни, то запишем ОДЗ:
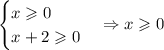
Также заметим, что в левой части записано произведение двух неотрицательных выражений. Значит, правая часть уравнения также неотрицательна:
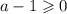
Таким образом, при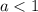 
уравнение не имеет корней.
Предположим, что . Тогда:
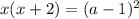
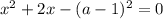
Проверим, удовлетворяют ли найденные корни ОДЗ.
Для первого корня получим:
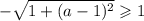
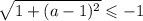
Однако, квадратный корень не может принимать отрицательных значений. Значит, рассматриваемое выражение не является корнем уравнения ни при каких значениях параметра 
.
Для второго корня получим:
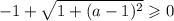
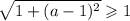
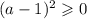
Последнее условие выполняется при любых значениях параметра . Но как отмечалось ранее, уравнение может иметь корни только при . Значит, данное выражение является корнем уравнения при .
при 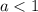: нет корней,
при : 
Объяснение:
1. Какие из точек М(6;1), К(-6;-5), А(0;-2), С(-1;3) принадлежат графику уравнения х – 2у = 4 ?
Чтобы установить принадлежность точки графику, нужно значения х и у (координаты точки) подставить в уравнение. Если левая часть будет равна правой, то принадлежит, и наоборот.
М(6;1)
х-2у=4
6-2*1=4
4=4, принадлежит
К(-6;-5)
-6-2*(-5)=-6+10=4
4=4, принадлежит
А(0;-2)
0-2*(-2)=4
4=4, принадлежит
С(-1;3)
-1-2*3=-7
-7≠4, не принадлежит.
2. Построить график уравнения х + 5у = 5
3. Построить график уравнения 2х -3у = 9
Прежде, чем строить графики, нужно уравнения преобразовать в более удобный для вычислений вид:
х+5у=5 2х-3у=9
5у=5-х -3у=9-2х
у=(5-х)/5 3у=2х-9
у=(2х-9)/3
Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Таблицы:
х -5 0 5 х -3 0 3
у 2 1 0 у -5 -3 -1
S=a*b
2a+2b=30
a*b=56
a=56/b
2*56/b+2b=30
b^2-15b+56=0
D=1 b=7 и b=8
a=56/b a=7 и a=8 , что, по сути, одно и тоже.
ответ: 8 и 7