при х= 4 выражение принимает своё наименьшее значение, равное 1.
Объяснение:
Рассмотрим квадратичную функцию
у = х²-8х+17.
Её графиком является парабола, ветви которой направлены вверх, т.к. а=1, 1>0.
Своего наименьшего значения функция достигает в вершине параболы.
х вершины = -b/2a = 8/2=4;
yвершины = 4²-8•4+17 = 1.
Получили, что 1 - наименьшее значение функции, которое она принимает при х=4, следовательно, функция принимает лишь положительные значения, что и требовалось доказать.
Насколько я понял задачи нужны просто на кинематику для 7-9 классов)
1) Мальчик ударил по шайбе клюшкой и сообщил ей скорость 30 м/с. Через время t=3 с скорость шайбы (она движется прямолинейно) равна 21 м/с. Найти ускорение шайбы.
Решение очень простое, введем ось Ox вдоль движения шайбы. За положительное конечно же примем направление вектора начальной скорости
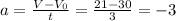 м/с^2
м/с^2
ответ: 3 м/с^2 (по модулю)
2) Изъеженная задача.
Два поезда движутся равномерно друг за другом. Скорость первого 90 км/ч, а другого 60 км/ч. Найти скорость первого относительно второго.
Тут опять же вводим ось Ox.
По закону сложения скоростей, неизвестное
 км/ч
км/ч
ответ: 30
x² - 8x + 17
Запишем это выражение в виде :
x² - 8x + 17 = x² - 8x + 16 + 1 = (x - 4)² + 1
1) (x - 4)² ≥ 0 , прибавив к значению этого выражения единицу, получим или 1, или какое- то положительной число. То есть это выражение может принимать только положительные значения.
2) Наименьшее значение этого выражения равно 1 при x = 4.