Если каждое слагаемое делится на некоторое число, то и вся сумма делится на это число.
Если одно слагаемое делится на некоторое число, а другое слагаемое не делится на это число, то и вся сумма не делится на это число.
1.
Пусть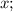 
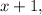
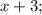
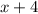- пять последовательных натуральных чисел, тогда их сумма равна:
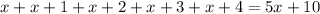
Очевидно, что каждое слагаемое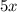 
и 
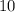делится на 5, а это означает, что вся сумма делится на 5.
Доказано.
2.
Пусть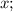 
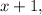
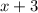- четыре последовательных натуральных числа, тогда их сумма равна:
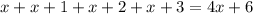
Очевидно, что первое слагаемое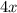 
делится на 4, а второе слагаемое 
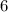не делится на 4, это означает, что вся сумма не делится на 4.
Доказано.
3.
Пусть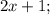 
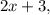
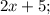
- четыре последовательных нечётных натуральных числа, тогда их сумма равна:
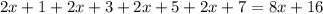
Очевидно, что каждое слагаемое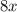 
и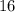 
делится на 8, а это означает, что вся сумма делится на 8.
Доказано.
4.
Пусть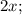 
; 
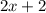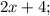
- четыре последовательных чётных натуральных числа, тогда их сумма равна:
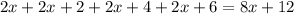
Очевидно, что каждое слагаемое 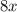и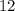 
делится на 4, а это означает, что вся сумма делится на 4.
Доказано.
p = 0,55; q = 1-p = 0,45; n = 6; m = 4
P(m,n) = C(m,n)*p^m*q^(n-m) =
P(4,6) = C(4,6)*(0,55)^4*(0,45)^2 = 6*5/2*0,0915*0,2025 = 0,278
2) Тоже по формуле Бернулли
p = 26/30 = 13/15; q = 1-p = 2/15; n = 5.
Вероятность ответить на 3 вопроса из 5: m = 3
P(3,5) = C(3,5)*(13/15)^3*(2/15)^2 = 5*4/2*0,651*0,178 = 0,116
Вероятность ответить на 4 вопроса из 5: m = 4
P(4,5) = C(4,5)*(13/15)^4*(2/15)^1 = 5*0,564*0,133 = 0,376
Вероятность ответить на 5 вопросов из 5: m = 5
P(5,5) = C(5,5)*(13/15)^5*(2/15)^0 = 1*0,489*1 = 0,489
Итоговая вероятность сдать экзамен
P = P(3,5) + P(4,5) + P(5,5) = 0,116 + 0,376 + 0,489 = 0,981