Есть 12 вариантов выбора книг для покраски по количеству книг в каждом цвете (красный, зеленый, коричневый)
1 1 10
1 2 9
1 3 8
1 4 7
1 5 6
2 2 8
2 3 7
2 4 6
2 5 5
3 3 6
3 4 5
4 4 4
Им соответствуют количество вариантов выбора книг по их числу, например, первому, 12!/(10!*2!)*2!/(1!*1!)=66*2=132. Их надо посчитать.
И каждому набору соответствует число возможных перестановок по цветам. Если все числа в наборе разные, то 3!=6, если две одинаковые, до 3!/(2!*1!)=3, если все одинаковые (последний случай) , то 3!/(3!*0!)=1.
Затем количество вариантов выбора книг для каждого набора надо умножить на количество перестановок в наборе (то есть, для первого получится 132*3=396), и полученные числа сложить. Получится 519156.
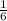
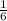- 1 =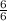 
- 1 = 1-1=0
task/29760192 cos(3x/2)*cos(x/2) -1 > (1/2) * (1 -√3) *cosx
Решение : cos(3x/2)*cos(x/2) -1 > (1/2) * (1 -√3) *cosx ||*2||
2cos(3x/2)*cos(x/2) -2 > (1 -√3) *cosx ;
cos2x+cosx - (1 -√3) *cosx - 2 > 0 ;
2cos²x -1 +cosx - cosx +(√3) *cosx - 2 > 0 ;
2cos²x +(√3) *cosx -3 >0 ⇔ ( cosx +√3 )(2cosx -√3 ) >0 ||cosx +√3 >0 ||⇔ cosx > (√3) /2 ⇒ 2πn - π / 6 < x < π / 6 + 2πn , n ∈ ℤ (объединение интервалов )
ответ : x ∈ ( - π / 6 + 2πn ; π / 6 + 2πn ) , n ∈ ℤ.
P.S. 2cos²x +(√3) *cosx -3 = 0. D=(√3)²+4*2*(-3) =27 =(3√3)² ⇒√D =3√3)
cosx₁ = - √3 < - 1 → посторонний корень ; cosx₂ =(√3) / 2. * * *