![1.\; \; \sqrt{-a^5}=\sqrt{a^4\cdot (-a)}=\sqrt{(a^2)^2\cdot (-a)}=|a^2|\cdot \sqrt{-a}=\\\\=\Big [\; -a\geq 0\; \; \to \; \; a\leq 0\; \Big ]=a^2\cdot \sqrt{-a}](/tpl/images/0700/7323/76e51.png)
![2.\; \; b\geq 0\; ,\; \; \sqrt{-a^3\cdot b^6}=\sqrt{a^2\cdot (-a)\cdot (b^3)^2}=|a|\cdot |b^3|\cdot \sqrt{-a}=\\\\=\Big [\; -a\geq 0\; \; \to \; \; a\leq 0\; \; \to \; |a|=-a\; \; ;\; \; b^3\geq 0\; \; \to \; \; |b^3|=b^3\; \Big ]=\\\\=-ab^3\sqrt{-a}](/tpl/images/0700/7323/74d83.png)
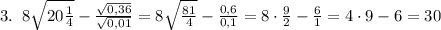
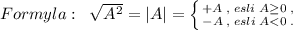
В примере √5+√6 не пишут ответ, т.к.:
Квадратные корни люди не умеют складывать примеры так и оставляют без ответа :
7+√3 ( не пишут ответ, можно только приближённо)
√5 - √7 ;( не пишут ответ) √3 +√11 ( не пишут ответ)
Складывать корни можно только одинаковые :
а) √5 + 4√5 = 5√5 ( походит на пример х+4х=5х)
б) √3 - 4√3 = -3√3 ( походит на пример х -4х= -3х)
в) 2√3 + 4√3 -7 √5 = 6√3 -7 √5 ( походит на пример
2а + 4а -7 у = 6а -7 у)
√18 +√50 -√8 ( под корнем все числа разные и такие примеры не решаются, но под корнем можно сделать одинаковые числа) :
√18 +√50 -√8 = √9*2 +√25*2 -√4*2 =√2 +5√2 -2√2 =6√2
Вот все правила по складываниям корней, которые нужно знать.
Надеюсь
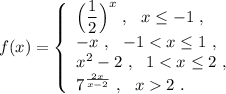
Исследуем поведение функции вблизи точек, где её аналитическое выражение меняется . Найдём левосторонние и правосторонние пределы в точках х= -1, х=1 , х=2 .
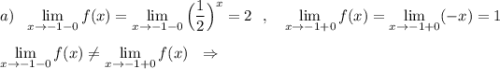
При х= -1 функция имеет разрыв 1 рода .

При х=1 функция непрерывна.
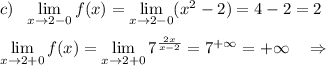
При х=5 функция имеет разрыв 2 рода .
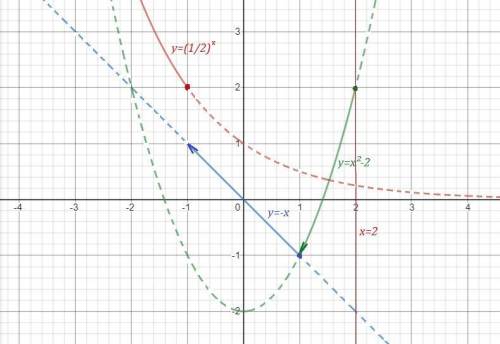
График функции нарисован сплошными линиями.
На 1 рисунке нет чертежа функции при х>2 , для которого прямая х=2 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>2 сплошной линией..
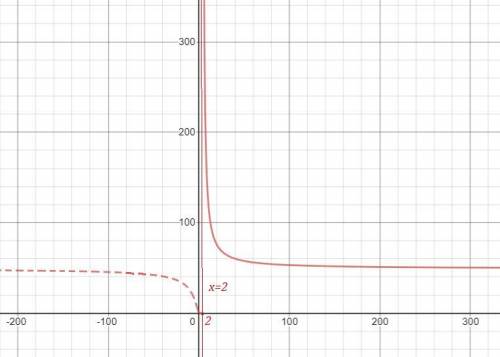
Решение задания приложено