разница арифметичесской прогрессии равна
d=a[2]-a[1]=4.2-4.6=-0.4
общий член арифметичесской прогрессии равен
a[n]=a[1]+d*(n-1)
a[n]=4.6-0.4*(n-1)=4.6-0.4n+0.4=5-0.4n
найдем сколько положительных членов в данной арифметичесской прогрессии
5-0.4n>0
-0.4n>-5
n<5:0.4
n<12.5
12 наибольшее натуральное число, удовлетворяющее неравенство
значит первые 12 членов данной арифметичесской прогрессии положительные
Сумма первых n членов арифметической прогресси равна
S[n]=(2*a[1]+(n-1)*d)/2*n
S[12]=(2*4.6+(12-1)*(-0.4))/2*12=28.8
отвте: 28.8
а) b = 18 б) b = 10 в) y=20 г) y = 1,2
д) a = 9 е) a = 24 ж) x = 1,4 з) x = 0,6
Объяснение:
Основное свойство пропорции: произведение крайних членов пропорции равно произведению средних членов пропорции.
a : b = c : d ⇒ ad = bc
а) 2 : 9 = 4 : b; 2b = 9*4; 2b = 36; b = 36 : 2; b = 18;
б) 15 : b = 3 : 2; 15*2 = b*3; 30 = 3b; b = 30 : 3; b = 10;
в) 3 : 2,1 = y : 14; 3 * 14 = 2,1y; 42 = 2,1y; y = 42 : 2,1; y = 20;
г) y : 2,4 = 3 : 6; 6y = 2,4*3; 6y = 7,2; y = 7,2 :6; y = 1,2;
д) 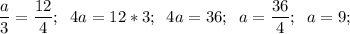
е) 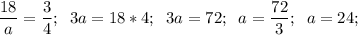
ж) 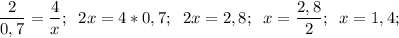
з) 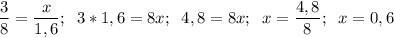
9-x²=0
x²=9
x=-3∉[1;4]
x=3∈[1;4]
y(1)=-9-1=-10 наим
y(3)=-3-3=-6 наиб
y(4)=-2,25-4=-6,25