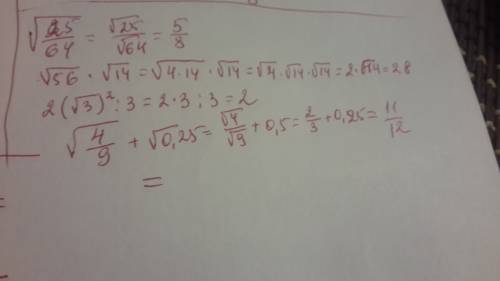
Возьмем ваше же уравнение
lx+2l+lxl+lx-2l=4
Левую и правую части уравнения рассматриваем как функции.
f(x)=lx+2l+lxl+lx-2l и g(x)=4
С g(x) все понятно. Это прямая y=4, параллельна Ox.
С f(x) разбираемся. Это кусочная функция. Найдем нули подмодульных выражений:
x+2=0 ⇒ x=-2, x-2=0 ⇒ x=2, x=0.
Имеем интервалы (-∞; -2); [-2; 0); [0; 2); [2; +∞). Запишем равносильный переход:
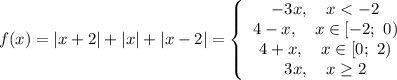
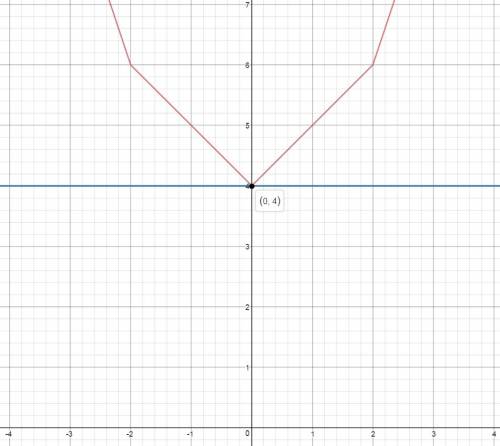
Построение графика на этом этапе элементарно. Из системы можно видеть, что функция f(x) четная. Достаточно построить или левую или правую ее часть, остальное отзеркалить. Готовый рисунок приложен.
а) 4x² - 4x - 15 < 0
D = b² - 4ac = 16 + 4*4*15 = 16 + 240 = 256
x₁ = (-b + √D) / 2a = (4 + 16) / 8 = 20 / 8 = 2,5
x₂ = (-b - √D) / 2a = (4 - 16) / 8 = -12 / 8 = -1,5
(x - 2,5)(х + 1,5) < 0
{ x < 2,5
{ x < -1,5
ответ: (-1,5; 2,5)
б) x² - 81 > 0
(x - 9)(x + 9) > 0
{ x > -9
{ x > 9
ответ: (-9; 9)
в) x² < 1,7х
x² - 1,7х < 0
х(x - 1,7) < 0
{ x < 0
{ x < 1,7
ответ: (0; 1,7)
г) x( x + 3) - 6 < 3 (x + 1)
x² + 3x - 6 - 3x - 3 < 0
x² - 9 < 0
(x - 3)(x + 3) < 0
{ x < -3
{ x < 3
ответ: (-3; 3)
28
2
13/18