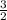
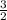
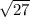
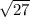
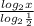 + 2 = 0
+ 2 = 0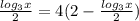
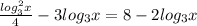
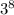
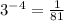
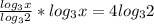
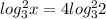
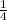
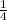
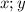 из набора множеств от -100 до 100 , то нужно найти
из набора множеств от -100 до 100 , то нужно найти 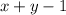 . Очевидно что если мы будет брать крайние числа , по закону перемещения ничего не изменится , можно даже решить ослабленную версию такой задачи где требуется найти сумму
. Очевидно что если мы будет брать крайние числа , по закону перемещения ничего не изменится , можно даже решить ослабленную версию такой задачи где требуется найти сумму 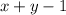 из множество чисел от 1 до 25 и.т.д .
из множество чисел от 1 до 25 и.т.д . 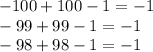 уже 100 операций проделано , теперь осталось 100
уже 100 операций проделано , теперь осталось 100 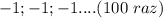
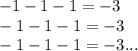 50 раз , следовательно 50 операций
50 раз , следовательно 50 операций
отсюда формула для члена прогрессии с номером n нас
an=a1+d(n-1)
у нас
аn+1=a1+d*n
an+4=a1+d*(n+3)=a1+d*n+3d
a1+d*n=a1+d*n+3d d=0 это странно. Но иначе не мог бы n+1 член равняться n+4 -му. Так-что это просто ряд чисел равных -9
сумма 16-ти членов -9*16=-144
или ошибка в условии...