1)
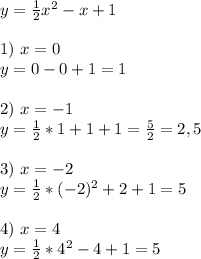
2)
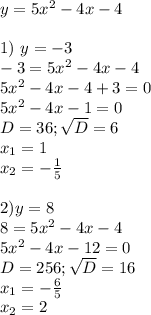
3)
1) y=x²+10 - парабола , поднятая на 10 точек вверх, координаты вершины (0;10)
2) y=x²-5 - парабола, на 5 точек вниз, координаты вершины (0;-5)
3) y=(x+7)² - парабола, передвинутая на 7 точек влево, вершина (-7;0)
4) y=(x-8)²-парабола, передвинутая на 8 точек вправо, вершина (8;0)
4) y=x²
1) y=x²+5
2)y=x²-4
3)y=(x-3)²
4)y=(x+6)²
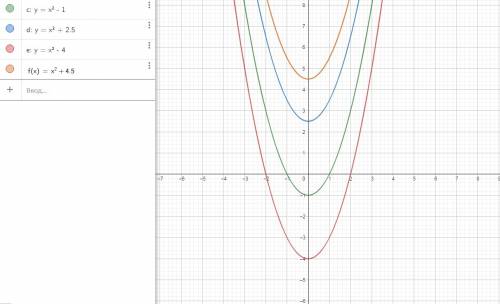
5)
На фото, c Ox пересекается график функции y=x²-4.
Точки пересечения с Ox (-2;0) и (2;0)
И y=x²-1
Точки пересечения с Ox (-1;0) и (1;0)
С Oy : y=x²-1, (0;-1)
y=x²+2,5 , (0;2,5)
y=x²-4, (0;-4)
y=x²+4,5, (0;4,5)
(x+3)^2+|x+2|≥1
Надеюсь, Вы знаете "галку" - график модуля. В нашем случае галка смещена на 2 единицы влево.
На участках x≤ - 3 и x≥ - 1 |x+2|≥1⇒ неравенство выполнено.
Параболу Вы также должны знать. В нашем случае она смещена на три 1 влево⇒она не ниже 1 на участках x≤ - 4 и x≥ - 2.
Значит, единственным проблемным промежутком является (-3;-2).
На этом участке модуль раскрывается с минусом; получается неравенство
x^2+6x-x+6≥0;
x^2+5x+6≥0;
(x+2)(x+3)≥0;
x∈(-∞;-3]∪[-2;+∞).
Значит, на участке (-3;-2) неравенство не выполняется.
ответ: (-∞;-3]∪[-2;+∞)
P.S. Конечно, я пижонил, надо было просто рассмотреть два случая раскрытия модуля x≤ - 2 и x≥ - 2 и в каждом случае решить квадратное неравенство, но в половину четвертого ночи я могу заставить себя работать только по пижонски. Так что не обижайтесь.