Многочлен-это сумма одночленов. Таким образом, необходимо просто раскрыть скобки. В результате получим:
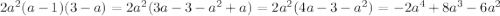
x2 + 4x + 8 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = 42 - 4·1·8 = 16 - 32 = -16
Так как дискриминант меньше нуля, то уравнение не имеет действительных решений.
4x2 - 12x + 9 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = (-12)2 - 4·4·9 = 144 - 144 = 0
Так как дискриминант равен нулю то, квадратное уравнение имеет один действительных корень:
x = 122·4 = 1.5
3x2 - 4x - 1 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = (-4)2 - 4·3·(-1) = 16 + 12 = 28
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x1 = 4 - √282·3 = 23 - 13√7 ≈ -0.21525043702153024
x2 = 4 + √282·3 = 23 + 13√7 ≈ 1.5485837703548635
2x2 - 9x + 15 = 0 Найдем дискриминант квадратного уравнения: D = b2 - 4ac = (-9)2 - 4·2·15 = 81 - 120 = -39 Так как дискриминант меньше нуля, то уравнение не имеет действительных решений.1) а) a^2*b + a*b^2 = ab*(a+b) = 4*5 = 20
б) a^2 + b^2 = a^2 + 2ab + b^2 - 2ab = (a+b)^2 - 2ab = 5^2 - 2*4 = 17
2) а) 9^n - 2*3^n - 3 = 0
(3^n - 3)(3^n + 1) = 0
3^n + 1 > 0 при любом n.
3^n = 3
n = 1
б) 25^n - 2*5^n - 25 = 0
25^n - 2*5^n + 1 - 26 = 0
(5^n - 1)^2 - 26 = 0
(5^n - 1 - √26)(5^n - 1 + √26) = 0
5^n - 1 + √26 > 0 при любом n.
5^n = 1 + √26
n = log5 (1 + √26)
Если вы не поняли этого решения, значит, в задаче опечатка.
3) а) 6^31+6^30*5+6^29*5^2+ ... +6*5^30+5^31+5^32 =
= (6^32 - 5^32) / (6 - 5) + 5^32 = 6^32 - 5^32 + 5^32 = 6^32
б) 5^20+5^19*4+5^18*4^2+ ... +5*4^19+4^20-5^21 =
= (5^21 - 4^21) / (5 - 4) - 5^21 = 5^21 - 4^21 - 5^21 = -4^21
=2a^2*(4a-a^2-3)=-2a^4+8a^3-6a^2