(x+1)(x^2-x+1)-x(x+3)(x-3) Упростим данное выражение, для этого раскроем скобки. Также заметим, что (x+1)(x^2-x+1) - это формула сокращенного умножения: a³+b³=(a+b)(a²-ab+b²) , где, в нашем случае, a - это x, а b - это x, таким образом, (x+1)(x^2-x+1)=x³+1.
Заметим, (x+3)(x-3) - тоже формула сокращенного умножения - разность квадратов
(x+3)(x-3)=x²-9/ Преобразуем наше выражение, дораскрываем скобки:
(x+1)(x^2-x+1)-x(x+3)(x-3)=x³+1-x(x²-9)=x³+1-x³+9x=9x+1.
Найдем значение выражение при x=1:
9*1+1=10.
Удачи!
Объяснение:
2; - 11
Объяснение:
x⁴ = (9x - 22)²
x⁴ - (9x - 22)² = 0
(x²)² - (9x - 22)² = 0
Разложим на множители по формуле разности квадратов:
(x² - (9x - 22))(x² + (9x - 22)) = 0
(x² - 9x + 22)(x² + 9x - 22) = 0
Произведение равно нулю, если один из множителей равен нулю.
1) x² - 9x + 22 = 0
D = 81 - 88 = - 7 < 0 - нет корней
2) x² + 9x - 22 = 0
D = 81 + 88 = 169

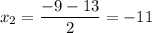
_______________________________
Думаю, ошибка у Вас была в первом преобразовании, вероятно, вы извлекали корень из левой и правой части и делали это неправильно, надо было так:
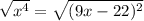
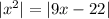
И дальше надо было решать уравнение с модулем.
Но разложение на множители исходного уравнения проще.