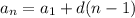
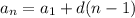
b)
3
x
+3
x+2
<270
3
x
+3
2
∗3
x
<270
3
x
+9∗3
x
<270
10∗3
x
<270 ∣:10
3
x
<27
3
x
<3
3
x<3.
ответ: x∈(-∞;3).
h)
\4*4^x-2\geq 7*2^x\\4*(2^2)^x-7*2^x-2\geq 0\\4*2^{2x}-7*2^x-2\geq 0\\\
4∗4
x
−2≥7∗2
x
4∗(2
2
)
x
−7∗2
x
−2≥0
4∗2
2x
−7∗2
x
−2≥0
Пусть 2ˣ=t ⇒
\4t^2-7t-2\geq 0\\4t^2-8t+t-2\geq 0\\4t*(t-2)+(t-2)\geq 0\\(t-2)*(4t+1)\geq 0\\(2^x-2)*(4*2^x+1)\geq 0\\4*2^x+1 > 0\ \ \ \ \Rightarrow\\2^x-2\geq 0\\2^x\geq 2\\2^x\geq 2^1\\x\geq 1.\
4t
2
−7t−2≥0
4t
2
−8t+t−2≥0
4t∗(t−2)+(t−2)≥0
(t−2)∗(4t+1)≥0
(2
x
−2)∗(4∗2
x
+1)≥0
4∗2
x
+1>0 ⇒
2
x
−2≥0
2
x
≥2
2
x
≥2
1
x≥1.
ответ: x∈[1;+∞).
x^2 + 1 = 7 - x
x^2 + x - 6 = 0
(x + 3)(x - 2) = 0
Границы: -3 и 2
Прямая y = 7 - x лежит выше параболы, поэтому вычитаем из нее.