Рассшифруем условие задачи
Итак, участок АС:
Это расстояние мотоциклист проехал за время t час, со скоростью 90 км/час
тогда автомобиль проехал это расстояние за t+1 час со скоростью х км/час
Так как они встретились в точке С то их пути равны: получили первое уравнение
90*t=(t+1)*х
Далее мотоциклист поехал обратно ( и как не странно АС=СА) значит времени затратил тоже t час. И за это время автомобиль доехал до B
Значит на весь путь автомобиль потратил t+1+t=2t+1 час и двигался со скоростью х км/час и проехал путь 300км
Получили второе уравнение
x*(2t+1)=300
решим нашу систему

из первого уравнение выразим х
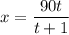
подставим во второе
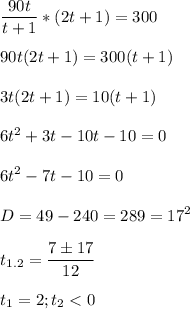 .
.
Значит время на путь от АС 2 часа
Расстояние 90*2=180 км
Объяснение:Находим критические точки данной функции.
Для этого находим производную данной функции и находим точки, в которых эта производная обращается в 0.
у' = (-х^2 + 6х + 7)' = -2x + 6.
-2x + 6 = 0;
2x = 6;
x = 6 / 2 = 3.
Следовательно, точка х = 3 является критической точкой данной функции.
Находим значение второй производной данной функции в точке х = 3.
у'' = (-2x + 6)' = -2.
Так как вторая производная данной функции отрицательна во всех точках, то она отрицательна и в точке х = 3, следовательно, в этой точке функция у = -х^2 + 6х + 7 достигает своего локального максимума.
Следовательно, данная функция возрастает на промежутке (-∞; 3) и убывает на промежутке (3; +∞).
ответ: данная функция убывает на промежутке (3; +∞).
10
Объяснение: