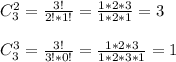
Попробую выразить х и у через z и подставить в первое уравнение.
Умножим второе уравнение на 2. Получим
8х+4у+10z=4/3. (*)
Из первого уравнения вычтем уравнение (*).
Получаем
-2х-3z=-1/3.
Умножаем обе части на (-3).
6х+9z=1
6x=1-9z
x=1/6-1,5z
Подставим 6х в первое уравнение и выразим у.
1-9z+4y+7z=1
1-2z+4y=1
4y-2z=0
4y=2z
y=0,5z
Если все работают вместе до завершения работы, то все работают одинаковое время. Пусть они работают t часов. Тогда уравнение выглядит следующим образом
t*(x+y+z)=1 (**)
Подставим, выраженные через z значения х и у в уравнение (**).
t*(1/6-1,5z+0,5z+z)=1
Все слагаемые, содержащие z сокращаются.
t*1/6=1
Умножим обе части на 6.
t=1*6
t=6 часов.
ответ: если бы все трое каменщиков работали вместе, то за 6 часов закончили бы работу.
10^2=100
8.8*1000+5.5*100=8800+550=9350