А (0; -4); B (0; 6).
Объяснение:
Задание.
Найдите координаты точки пересечения OY графиков линейных функций y=2x-4 и y=-3x+6 с решением, решение объясните.
Решение с объяснением.
В точке пересечения графика линейной функции с осью OY координата х всегда равна нулю.
А чтобы найти координату y точки пересечения графика линейной функции с осью OY, необходимо в заданное уравнение линейной функции вместо х подставить 0 (ноль) и рассчитать, чему равен у, когда х = 0.
1) Подставляем в уравнение y=2x-4 вместо х его значение, равное нулю. Получаем:
у = 2*0 - 4 = -4.
Это значит, что если х = 0, то у = - 4.
Обозначим буквой А точку пересечения графика линейной функции y=2x-4 с осью ОY. Тогда ответ можно записать так: А (0; -4). Здесь в круглых скобках указаны координаты точки А: на первом месте - координата х, а на втором месте - координата у.
2) Второе задание выполняем аналогично. Подставляем в уравнение y=-3x+6 вместо х его значение, равное нулю.
Получаем: у = -3*(0) + 6 = 6.
Это значит, что если х=0, то у =6.
Обозначим буквой B точку пересечения графика линейной функции y=-3x+6 с осью ОY.
Тогда ответ можно записать так:
B (0; 6).
⠀ ⠀ ⠀ ⠀ ⠀ ⠀ ⠀ ⠀— Здравствуйте, GraceMiller!
• ответ:
Упрощением выражения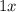 
, или же выражения 
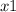будет являться 
.
• Как и почему?
Для того, чтобы нам выяснить, действительно ли это так, то мы должны знать два простых правила:
⠀• 1. Про выражение 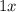: Когда член 
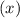имеет коэффициент 
, записывать его НЕ ОБЯЗАТЕЛЬНО, ведь коэффициент, равный , НЕ ЗАПИСЫВАЕТСЯ.
⠀• 2. Про выражение 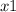: Любое выражение, умноженное на число , НЕ ИЗМЕНЯЕТСЯ.
• Вывод: Таким образом, для достижения упрощения выражения 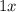или 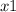мы получаем ответ .
⠀ ⠀ ⠀ — С уважением, Ваша EvaVosSavant! :)
Пусть t = sinx, t ∈ [-1; 1].
2t² - t - 1 = 0
D = 1 + 4•2 = 3²
t1 = (1 + 3)/4 = 1
t2 = (1 - 3)/4 = -1/2
Обратная замена:
sinx = 1
x = π/2 + 2πn, n ∈ Z
sinx = -1/2
x = (-1)ⁿ+¹π/6 + πn, n ∈ Z.
2) sin2x + 2cosx = 0
2sinxcosx + 2cosx = 0
cosx(sinx + 1) = 0
cosx = 0
x = π/2 + πn, n ∈ Z
sinx = -1
x = -π/2 + 2πn, n ∈ Z
3) sin(2x - π/3) = -1
2x - π/3 = -π/2 + 2πn, n ∈ Z.
2x = -π/6 + 2πn, n ∈ Z
x = -π/12 + πn, n ∈ Z