Просто подставлять и решать слишком муторно и глупо. Поэтому, сначала упростим наше выражение.
N° 1 — «Раскрытие скобок». Если дана скобка, а за ней сразу же число, это означает, что надо раскрыть скобки, умножив число вне скобки в каждое число в скобке по отдельности, учитывая знаки:
3(5m – 4n) – 4(3m – 2n) =
= 15m – 12n – 12m + 8n
N° 2 — «Подобные слагаемые». Подобные слагаемые — это те, которые имеют после себя одинаковую букву — переменную. Учитывая знаки, мы должны их «сократить»:
15m – 12n – 12m + 8n =
3m – 4n
Мы молодцы! Наше выражение полностью сокращено! Но это ещё не все. Нам надо вычислить значение выражения, подставив числа, данные в условии вместо подходящих букв.
3m – 4n
3 ⋅ (– 0,2) – 4 ⋅ 0,7 = – 0,6 – 2,8 = – 3,4
ответ: – 3,4
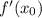производная функции в данной точке. А 
точка касания по иксу.
мы должны найти производную общего типа этой функции.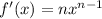
- где n это степень.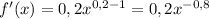
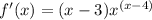
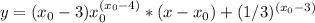
и получаешь уравнение касательной.
Вроде так
В Калькуляторе посчитал.