Конечно можно занятся исследованием функций, находить производные, но тут максимально упрощена задача.
1) просто построй функцию на отрезке [-2;1] подставив точки -2, -1, 0, 1. Этого будет достаточно, чтобы увидеть, что наименьшее значение будет в точке (0;0) равное 0, а наибольшее в точке (-2;64) равное 64. Так как графиком будет являтся суженная парабола.
2) то же самое. Чтобы узнать сколько корней, надо построить график левой части и правой части, и посмотреть есть ли у графиков точки пересечения. Сколько точек пересечения столько и корней.
построй график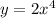 
на отрезке [-2;2]. Этого будет достаточно. График снова суженная парабола.
и график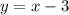 
на том же отрезке, а здесь будет прямая, которая уйдет вниз, и у нее не будет общих точек пересечения с параболой.
Значит корней здесь нет.
нр-не равно
ОДЗ: 2cosx-1нр0; 2cosxнр1; cosxнр1/2; xнр+-п/3+2пк (к=0,1,2,3,...,n); хнр+-п/3,+-п/3+2п,
+-п/3+4п,...
2sinx-корень3=0;sinx=корень3/2;x=(-1)^k*(п/3)+пк;x=п/3,-п/3+п,п/3+2п,-п/3+3п,...
выбираем значения удовлетворяющие ОДЗ:х=-п/3+п,-п/3+3п,...
х=-п/3+пк (к=1,3,5,...,)
ОДЗ:2sinx-1нр0;sinxнр1/2;хнр(-1)^k*п/6+пк (к=0,1,2,3,4,...);хнрп/6,-п/6+п,п/6+2п,-п/6+3п,...
2cosx-корень3=0;cosx=(корень3)/2;х=+-п/6+2пк;х=+-п/6,+-п/6+2п,+-п/6+4п,...
выбираем значения удовлетворяющие ОДЗ:х=-п/6,-п/6+2п,-п/6+4п,...
х=-п/6+2пк (к=0,1,2,3,4,5,...)
ОДЗ:1-соs(6x)нр0;cos6xнр1;6хнр2пк;хнр(п/3)к (к=0,1,2,3,4,5,...);хнр0,п/3,2п/3,п,...
sin6x=0;6x=пк;х=(п/6)к;х=0,п/6,п/3,п/2,2п/3,...
выбираем значения удовлетворяющие ОДЗ:х=п/6,п/2,...
х=(п/6)к (к=1,3,5,7,...)
A) 3(x - 2y) - 2(3x - y) = 3x - 6y - 6x + 2y = -3x - 4y;
Б) (2a - 3b)(a + b) - (a - b) = 2a^2 + +2ab - 3ab - 3b^2 - a + b = 2a^2 - -3b^2 - a + b - ab.
N 2.
A) 6ab - 3b2 = 6ab - 6b = 2b(3a - -3).
Б) ac + bc - 3a - 3b = c(a + b) - 3(a + +b) = (c - 3)(a + b).