Дано:
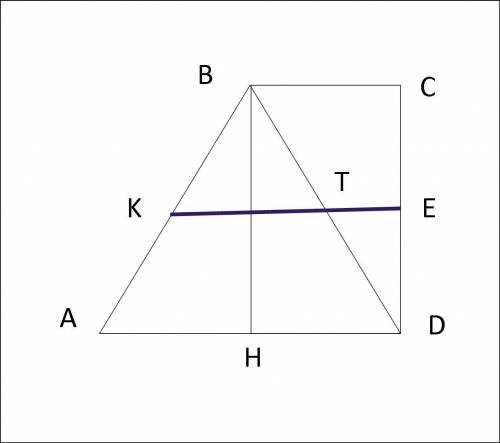
ABCD - трапеция;
∠ADC=∠BCD=90°
AB=BD=AD=5 см
KE—средняя линия
Найти КЕ
Решение
1) Проведем высоту ВН.
2) Рассмотрим четырёхугольник HBCD.
∠BCD=∠CDH =90° по условию;
∠BHD=90° по построению;
Учитывая, что сумма внутренних углов выпуклого четырёхугольника равна 360°, находим четвертый угол:
∠HBC=360°-(∠BHD +∠BCD+∠CDH)
∠HBC=360°- 3*90°=90°
Так как у четырёхугольника HBCD все углы прямые, то он является прямоугольником.
Следовательно, его противоположные стороны равны, т.е.
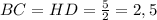 см
см
3) А теперь находим длину средней линии трапеции ABCD.
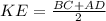
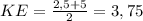
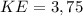 см
см
2) 11*4=44 (км) - расстояние между поселками.
ответ. 44 км.