Предположим, что х часов - это время работы первой бригады, тогда (х+4) часа - время работы второй бригады, примем всю работу за 1
согласно этим данным составим и решим уравнение для совместной работы:
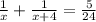 /·24x(x+4)
/·24x(x+4)
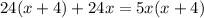
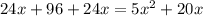
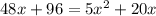
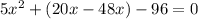
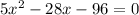
Cчитаем дискриминант:
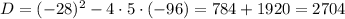
Дискриминант положительный
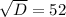
Уравнение имеет два различных корня:
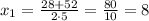
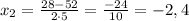
не удовлетворяет условию задачи, так как отрицательное время быть не может
х=8 (ч) - I бригада.
х+4=8+4=12 (ч) - II бригада.
Следовательно первая бригада заасфальтирует участок дороги за 8 часов, а вторая за 12 часов.
Предположим, что х часов - это время работы первой бригады, тогда (х+4) часа - время работы второй бригады, примем всю работу за 1
согласно этим данным составим и решим уравнение для совместной работы:
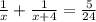 /·24x(x+4)
/·24x(x+4)
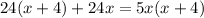
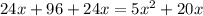
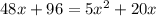
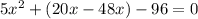
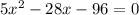
Cчитаем дискриминант:
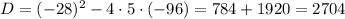
Дискриминант положительный
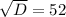
Уравнение имеет два различных корня:
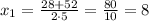
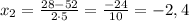
не удовлетворяет условию задачи, так как отрицательное время быть не может
х=8 (ч) - I бригада.
х+4=8+4=12 (ч) - II бригада.
Следовательно, первая бригада заасфальтирует участок дороги за 8 часов, а вторая за 12 часов.
Избавляемся от знаменателя
3x² + 11x + 4 = 3(3x-1)
3x² + 11x + 4 = 9x - 3
3x² + 11x - 9x + 4 + 3 = 0
3x² + 2x + 7 = 0
D = 4 - 112 = -108
Дискриминант меньше нуля. Корней нет.
2)
Избавимся от знаменателя:
7x - 21 + x² - 6x + 9 = 18
x² + 7x - 6x + 9 - 18 - 21 = 0
x² + x - 30
D = 1 + 120 = 121
x₁ =
x₂ =
Удачи!