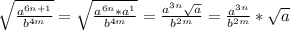Пусть исходный треугольник АВС с вершиной прямого угла в точке С. АС = 24 * Х , ВС = 7 * Х. Тогда по теореме Пифагора АВ = 25 * Х. Прямая пересекает катет АС в точке D, а катет АВ с точке Е. Треугольники АВС и ADE подобны (прямоугольные с общим острым углом). Тогда АЕ = 50 , AD = 48. В четырехугольник CDEB можно вписать окружность, то есть CD + EB = DE + BC 14 + 7 * X = 25 * X - 48 + 24 * X - 50 14 + 7 * X = 49 * X - 98 42 * X = 112 X = 8/3 см. Итак, катеты треугольника а = 56/3 и b = 64, гипотенуза 200/3 , а радиус вписанной окружности r = (a + b - c)/2 = (56/3 + 64 - 200/3)/2 = 8 см.
Первая картина стоит х руб, а вторая у руб. Первая картина продана на 20% дешевле,то есть за 80% от стоимости, что составляет 0,8x руб. Вторая картина продана на 20% дороже ,то есть за 120%, что составляет 1,2у руб. Цены уравнялись,значит 0,8x=1,2y x=1,2y/0,8 x=12y/8 x=(3/2)y=1,5у Значит первая картина стоила дороже второй в 1,5 раза.
№4.67
а)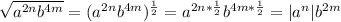
б)
в)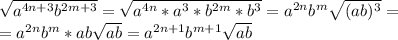
г)