а) 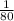
б) 324
Объяснение:
а) 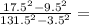
И числитель и знаменатель это формула сокращенного умножения, а точнее разница квадратов. Раскладывается следующим образом:
a² - b² = (a - b) × (a + b)
Сначала разберемся с числителем:
1) 17.5² - 9.5² = (17.5 - 9.5) × (17.5 - 9.5)
2) (17.5 - 9.5) × (17.5 - 9.5) = (8) × (27); (в конце скобки писать не обязательно, это я для наглядности)
Так и оставим пока что. Далее действия со знаменателем:
1) 131.5² - 3.5² = (131.5 - 3.5) × (131.5 + 3.5)
2) (131.5 - 3.5) × (131.5 + 3.5) = (128) × (135); (в конце скобки писать не обязательно, это я для наглядности)
Подставляем числитель и знаменатель:
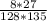
8 и 128 сокращаются. Так же 27 и 135 сокращаются:
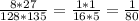
б) 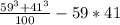
В числителе находится формула сокращенного умножения, а точнее сумма кубов. Раскладывается следующим образом:
а³ + b³ = (a + b) × (a² - ab + b³)
Разберемся с числителем:
1) 59³ + 43³ = (59 + 41) × (59² - 59 × 41 + 41²)
2) (59 + 41) × (59² - 59 × 41 + 41²) = (100) × (59² - 59 × 41 + 41²)
Так пока и оставим (100 не обязательно брать в скобки, это я для наглядности).
Поставим получившийся пример обратно в числитель:
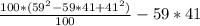
100 и 100 сокращаются:
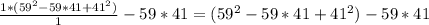
59² - 59 × 41 + 41² - 59 × 41 = 59² + 41² - 59 × 41 - 59 × 41 (от перемены мест слагаемых сумма не изменяется)
59² + 41² - 59 × 41 - 59 × 41 = 59² - 2 (59 × 41) + 41²
Это разложенный вид формули сокращенного умножения, а точнее квадрата разницы. Складывается следующим образом:
a² - 2ab + b² = (a - b)²
59² - 2 (59 × 41) + 41² = (59 - 41)² = 18² = 324
1. 3 минуты это 3/60 часа, или (1/20)часа. За 3мин., следовательно, страус пробегает 72*(1/20)=3,6 (км/ч) Это равно 3 км 600 метров
2. Поезд идёт со скоростью 162 км/ч. Сколько метров он проезжает за одну секунду? ответ: 45.
3. 144 км=144000м
1 час=60 минут=3600 секунд
Значит;
поезд за 3600 секунд проезжает 144000 км
тем самым
нам надо разделить скорость на время
14400:3600=40(м)
ответ:40 метров поезд проедет за 1 секунду
4. 1мм=1/1000м, 1.5мм/с=0.0015м/с
5.1. 3.6 км=3600м
2. 1час = 3600сек
3. 3,6 км в час=3600 м : 3600 сек = 1 м в сек.
2)(cos²(90°-α)-1)/cos(180°-α)=(sin²α-1)/(-cosα)=-cos²α/-cosα=cosα;
3)sin(π-α)/tg(π+α)=sinα/tgα=sinα/(sinα/cosα)=cosα;
4)tg(π-α)/ctg(π/2 -α)=-tgα/tgα=-1;
1)tg(π-α)=-tgα;
2)cos(360°-α)=cosα;
3)sin(90°-α)-cos(180°-α)+tg(180°+α)-ctg(270°-α)=
=cosα-(-cosα)+tgα-tgα=2cosα;
4)ctg(360°-α)=-ctgα;
5)ctg(π+α)=ctgα;
6)sin(360°+α)=sinα;
7)tg(360°+α)=tgα.