1. -15 ≤ 1-2у ≤ 0
2. 
Объяснение:
1. Т.к. в линейном выражении 1-2у перед у стоит знак "-", то при вычислении пределов возможных значений нужно либо поменять направление знаков больше (меньше) либо поменять местами подставляемые значения 1/2 и 8.
для 1/2 ≤ у: 1-2у ≤ 0
для у ≤ 8: 1-2у ≥ -15
Тогда: -15 ≤ 1-2у ≤ 0
2. Здесь перед у знак "+", но появилась нелинейная зависимость 4/у, поэтому нужно вычислить производную функции (4/у + у) и приравнять её к нулю, чтобы найти ее экстремум.
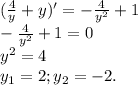
Но так как значение -2 не попадает в наш промежуток по условию, то это значение отбрасываем.
Значит, в точке у=2 имеем экстремум. Определим его значение:
для у=2: 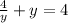 .
.
На остальных участках функция либо возрастает, либо убывает. подставим граничные значения из условия:
для у=1/2 : 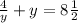
для у=8: 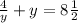 .
.
Т.е. имеем кривую с максимумами 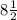 и минимумом 4.
и минимумом 4.
Тогда 
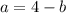 или
или 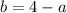 подставляем это во второе выражение и получаем обычное квадратное ур-ие.
подставляем это во второе выражение и получаем обычное квадратное ур-ие.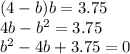
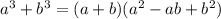
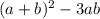
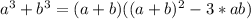
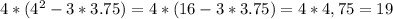
ответ: -8
Объяснение:
По формуле bn = b₁ * qⁿ⁻¹ преобразуем b₂, b₃, b₅:
b₂ = b₁ * q,
b₃ = b₁ * q²,
b₅ = b₁ * q⁴.
Заменим b₂, b₃, b₅ в данных выражениях и составим систему:
b₁ + b₂ + b₃ = b₁ + b₁*q + b₁*q² = b₁ * (1 + q + q²)
b₁ + b₃ + b₅ = b₁ + b₁*q² + b₁*q⁴ = b₁ * (1 + q² + q⁴)
b₁ не равно нулю (от противного, если b₁ = 0, то система не имеет решений); аналогично множители с q не равны 0, поэтому можно выполнить деление уравнений.
Поделим второе уравнение на первое:
В первом уравнении сократим на b₁, не равное нулю, и решим его отдельно относительно q:
Так как знаменатель не обращается в нуль (D < 0), то можно выполнить перемножение крест-накрест. Получим:
4q⁴ + 4q² + 4 = 7q² + 7q + 7,
4q⁴ - 3q² - 7q - 3 = 0,
4q⁴ + (- 6q³ + 6q³) - 3q² + (-6q² + 6q²) - 7q + (-2q + 2q) - 3 = 0,
(4q⁴ - 6q³) + (6q³ - 9q²) + (6q² - 9q) + (2q - 3) = 0,
2q³(2q - 3) + 3q²(2q - 3) + 3q(2q - 3) + (2q - 3) = 0,
(2q - 3)(2q³ + 3q² + 3q + 1) = 0,
(2q - 3)(2q³ + (2q² + q²) + (2q + q) + 1) = 0,
(2q - 3)((2q³ + 2q² + 2q) + (q² + q + 1)) = 0,
(2q - 3)(2q(q² + q + 1) + q² + q + 1) = 0,
(2q - 3)(2q + 1)(q² + q + 1) = 0,
Последняя скобка не обращается в ноль (D < 0), следовательно
q₁ = -0,5
q₂ = 1,5
q₂ не подходит по условию (так как геометрическая прогрессия бесконечно убывающая, то есть |q| < 1)
Вернёмся к системе:
Используя найденные значения b₁ и q, найдём сумму прогрессии по соответствующей формуле: