По определению, arcsin 4/5 - это угол α, синус которого равен 4/5.
Причем, это угол, принадлежащий интервалу [- π/2; π/2].
Т.е.
arcsin 4/5 = α, sinα = 4/5, α ∈ [- π/2; π/2].
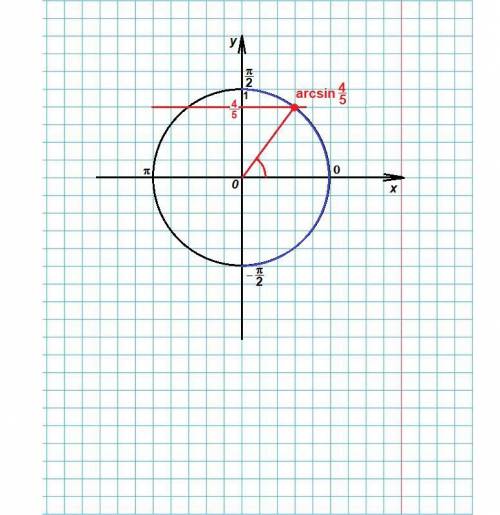
Построим этот угол на тригонометрической окружности.
Так как синус угла α - это ордината (координата у) точки, повернутой на угол α, то значение синуса 4/5 отмечаем на оси Оу.
Радиус окружности равен 1, поэтому делим его на 5 частей и отмечаем 4 из них.
Через полученную на оси Оу точку проводим горизонтальную прямую. Точка пересечения этой прямой с правой полуокружностью (с синей) и есть точка, соответствующая углу поворота α = arcsin 4/5.
х+6 м - длина бассейна
х+0,5+0,5=х+1 м - внешняя ширина дорожки
х+6+0,5+0,5=х+7 м - внешняя длина дорожки
S дор.=15 м²
Sбас.=х(х+6) м²
Sвн.=(х+1)(х+7) м² (тут нужен рисунок Прямоугольник в прямоугольнике--внутренний это бассейн, внешний - это стороны дорожки)
S дор.=Sбас. - S вн.
(х+1)(х+7) - х(х+6)=15
х²+8х+7 - х² - 6х=15
2х=15-7
2х=8
х=4(м) - ширина бассейна
4+6=10(м) - длина бассейна