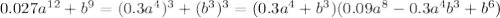
f(x) = 1/3 x^3 - x^2 + 6
Продифференциируем функцию
f ' (x) = x^2 - 2x
Приравняем производную к нулю
x^2 - 2x = 0
x (x - 2) = 0
x = 0, или x - 2 = 0
Из вышеназванного следует, что точки экстремума - это ноль и два
Возьмём число один, для проверки знаков в следующих промежутках
(минус бесконечность ; ноль), (ноль ; два), (два ; плюс бесконечность)
f ' (1) = 1 - 2 = - 1
Значит, что в среднем промежутке будет знак минус, в боковых плюс, из чего следует, что на промежутке от минус бесконечности до нуля производная функции положительна (сама функция возрастает), на промежутке от нуля до двух производная отрицательна (функция убывает), а на промежутке от двух до плюс бесконечности производная опять становится положительной, а функция возрастает...
Точка "ноль" - точка максимума
Точка "два" - точка минимума
Фатимка, дальше я не знаю, как решать, но надеюсь, что материал вам пригодится
По формуле вс угла:
4\sin x-16\cos x= \sqrt{4^2+4^4}\sin(x-\arcsin \frac{16}{ \sqrt{4^2+4^4} } )=4 \sqrt{17} \sin(x-\arcsin\frac{4}{\sqrt{17} })4sinx−16cosx=
4
2
+4
4
sin(x−arcsin
4
2
+4
4
16
)=4
17
sin(x−arcsin
17
4
)
Поскольку синус принимает свои значения - [-1;1], то
\begin{lgathered}-1 \leq \sin(x-\arcsin\frac{4}{\sqrt{17} } )\leq 1\\ \\ -4 \sqrt{17} \leq \sin(x-\arcsin\frac{4}{\sqrt{17} }) \leq 4 \sqrt{17}\end{lgathered}
−1≤sin(x−arcsin
17
4
)≤1
−4
17
≤sin(x−arcsin
17
4
)≤4
17
Наибольшее - 4 \sqrt{17}4
17
и наименьшее - (-4 \sqrt{17} )(−4
17
)