Решить систему линейных уравнений методом подстановки и методом сложения:
{
y
+
2
x
=
1
y
−
x
=
3
Решение методом подстановки.
{
y
+
2
x
=
1
y
−
x
=
3
⇒
{
y
=
−
2
x
+
1
y
−
x
=
3
⇒
{
y
=
−
2
x
+
1
(
−
2
x
+
1
)
−
x
=
3
⇒
{
y
=
−
2
x
+
1
−
3
x
−
2
=
0
⇒
{
y
=
−
2
x
+
1
x
=
−
2
3
⇒
{
y
=
7
3
x
=
−
2
3
y
=
2
1
3
;
x
=
−
2
3
Решение методом сложения.
{
y
+
2
x
=
1
y
−
x
=
3
Вычитаем уравнения:
−
{
y
+
2
x
=
1
y
−
x
=
3
(
y
+
2
x
)
−
(
y
−
x
)
=
1
−
3
3
x
=
−
2
x
=
−
2
3
Подставиим найденную переменную в первое уравнение:
(
−
2
3
)
+
2
x
=
1
y
=
7
3
y
=
2
1
3
;
x
=
−
2
3
Объяснение:
ответ: расстояние между пунктами 25 км
Рассуждай так: S=v*t ( расстояние равно скорость умноженная на время в пути), значит :
Пусть S₁= v*t- расстояние, которое преодолел за полчаса велосипедист( он отъехал из пункта В),
тогда S₂=u*t- которое преодолел за полчаса автомобилист ( а оно соcтоит из расстояния от пункта А до пункта В и плюс расстояние до места в котором он догнал велосипедиста( по - другому расстояние , которое велосипедист проехал за полчаса)
Составим выражение по условию задачи
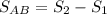 ,
,
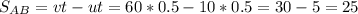 (км)
(км)
2cosx=-1
cosx=-1/2
x=+-arcos a+2kπ, k∈Z
x=+- 2π/3+2kπ
б) tg2x+1=0
tg2x=-1
2x=-π/4+2kπ
x=-π/8+kπ
в)sin(x/3+π/4)=-1
x/3+π/4=-π/2+2kπ
x/3=-π/2+π/4+2kπ
x/3=-π/4+2kπ
x=-3π/4+6kπ