Объяснение:
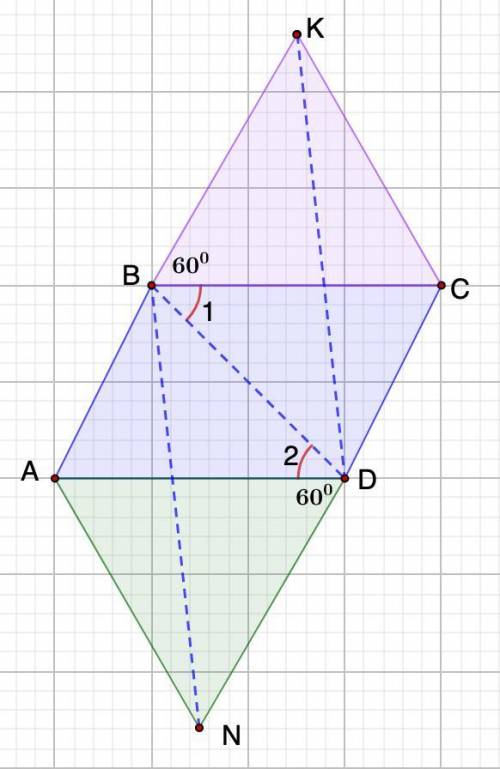
Дано: ABCD - параллелограмм.
ΔВКС и ΔAND - равносторонние.
Доказать: BKDN - параллелограмм.
Доказательство:
1. Рассмотрим ΔВКС и ΔAND - равносторонние.
Противоположные стороны параллелограмма равны.⇒ ВС = AD
⇒ ΔВКС = ΔAND (по трем сторонам, 3 признак)
⇒ BK = ND
2. ВС || AD (ABCD - параллелограмм)
∠1 = ∠2 (накрест лежащие при ВС || AD и секущей BD)
В равностороннем треугольнике углы равны 60°.⇒
∠DBK = ∠1 + 60°
∠BDN = ∠2 + 60°
⇒ ∠DBK + ∠BDN - накрест лежащие при BK и ND и секущей BD.
Если при пересечении двух прямых третьей накрест лежащие углы равны, то прямые параллельны.⇒ BK || ND
Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник - параллелограмм.⇒ BKDN — параллелограмм
2. Рассмотрим треугольник DBE.
Это равнобедренный треугольник, так как по условию BD = BE.
∠BDE = ∠BED, так как это углы при основании равнобедренного треугольника.
3. Определим ∠BDA и ∠BEC.
∠BDA и ∠BDE смежные, поэтому
∠BDA = 180° - ∠BDE.
Аналогично ∠BEC и ∠BED смежные, поэтому
∠BEC = 180° - ∠BED.
Так как ∠BDE = ∠BED, то и ∠BDA = ∠BEC.
4. Рассмотрим треугольники ABD и CBE.
Эти треугольники равны по двум сторонам и углу между ними:
BD = BE и AD = CE - по условию;
∠BDA = ∠BEC.
Следовательно, и стороны BA и BC равны.
Значит, треугольник ABC -равнобедренный.
Знаешь ответ?
По свойству треугольника больший угол лежит против большей стороны, следовательно больший угол А
АК - биссектрисса угла А
Теорема 9.
Биссектриса внутреннего угла треугольника делит противолежащую сторону на части, пропорциональные прилежащим сторонам, следовательно
12/15 = х/(18-х)
216=27х
х=8
бисектрисса делит основание на две части равные 8 и 10
Теорема d4.
(первая формула для биссектрисы) : Если в треугольнике ABC отрезок AL является биссектрисой угла A, то AL² = AB·AC - LB·LC.
В нашем случае АК" = АВ*АС - ВК*КС = 12*15-8*10=100
АК=10
ответ: биссектрисса равна 10см