Ошибка состоит в следующем: из (х - 2а)^2 = х^2 ошибочно сделан вывод, что х - 2а = х. Т.е. (х - 2а)^2 = х^2 => х - 2а = х.
На самом деле должно быть (х - 2а)^2 = х^2 => х - 2а = х (1) или х - 2а = -х (2)
(1) даст нам единственное решение а = 0 (отсюда и х = 0), а (2) - решение х = а.
Вариант (1) не подходит по условию, т.к. а должно быть отлично от 0.
Следовательно, единственным решением будет х = а, где а - не равно 0. Это совпадает с нашим исходным предположением, и никакого противоречия здесь нет.
1) 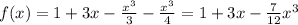
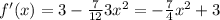
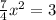
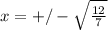
- + -
--------------'-------'---------->
-sqrt{12/7) sqrt(12/7)
Таким образом, x = -sqrt(12/7) - точка минимума,
x = sqrt(12/7) - точка максимума
2) 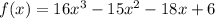
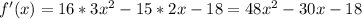
48x^2+30x-18=0
D = 4356
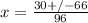
x=1
x =-3/8
+ - +
---------'-----------'----------->
-3/8 1
x = -3/8 - точка максимума
x = 1 - точка минимума
3) f(x) = sinx+x
f'(x) = cosx+1
Для любого х знак производной есть плюс и не меняется, т.к. |cosx|<=1
Значит f(x) монотонно возрастает на промежутке [0;2Pi]
4) f(x) = x + 2cosx
f'(x) = 1-2sinx
2sinx = 1
x = Pi/6 + Pik, k - целое
+ - +
-'-----'----------'--------------'
0 Pi/6 7Pi/6 2Pi
x = Pi/6 - точка максимума
x = 7Pi/6 - точка минимума
Теперь решим:
p1=1;p2=-5
ответ: при значениях 1 и -5