Объяснение:1)Бросают игральный кубик Определите вероятность появления на верхней грани: а) числа 1; общее число исходов в задаче n=6. Решаем все по формуле: Р(А)=m/n, благоприятных исходов m, число всех исходов n.
Число 1 встречается только один раз на кубике - значит число благоприятных исходов 1
P=1/6≈0,16(6) - вероятность того,что выпадет 1 очко.
б)числа 2; Число 2 встречается только один раз на кубике - значит число благоприятных исходов 1
P=1/6≈0,16(6) - вероятность того,что выпадет число 2.
в) нечетного числа; общее число исходов в задаче n=6. Благоприятствуют событию только такие исходы, когда выпадет грань с 1, 3 или 5 очками (только ytчетные), таких граней m=3. Тогда искомая вероятность равна P=3/6=1/2=0.5.
г)числа 1 или 2; Если при бросании игрального кубика выпало 1 или 2, т.е. удовлетворяют 2 исхода, m=2. Нужная вероятность равна P=2/6=1/3=0.333.
д) числа 8; благоприятный исход отсутствует (числа 8 нет на кубике), значит m=0, поэтому Р=0/6 =0
е) числа 1 или 2 или 3 или 4 или 5 или 6 . Благоприятных исходов может быть 6, значит m=6, тогда P=6/6=1.
2)подбрасывают монету. Определите вероятность выпадения: а) орла / Общее количество исходов n=2, благопрятный исход m=1, тогда Р=1/2=0,5
б) решки / Общее количество исходов n=2, благопрятный исход m=1, тогда Р=1/2=0,5
в)Орла и решки / Благоприятных исходов может быть 2, значит m=2, тогда P=2/2=1/.
г)ни Орла ни решки /благоприятный исход отсутствует , значит m=0, поэтому Р=0/2 =0
3)Из ящика Где находится 4 черных и 5 белых шаров вынимают Один шар .Какова вероятность того что вынут:
а) черный шар / m=4+5=9, n=4, Р=4/9
б) белый шар / m=4+5=9, n=5, Р=5/9
4) из 28 костей Домино выбирают наугад одну кость. Какова вероятность выбрать с суммы очков:
а) 0
б) 4
в)7
г) 13
5)Бросают два игральных кубика .Какова вероятность выпадения суммы чисел равной: Всего таких пар чисел будет n=6⋅6=36
а) 3 / Число 3 может выпасть 2 раза, значит Р=2/36=1/18
б) 9 / Число 9 может выпасть 4 раза, значит Р=4/36=1/9
в) 12 / Число 12 может выпасть 1 раз, значит Р=1/36
г)14 / Число 14 не может выпасть, m=0, значит Р=0/36=0
6)выполняет тест по математике ученик не успевает в определённое время выполнить одно задание Какова вероятность того что ученик угадать правильный ответ если из 5 возможных ответов только один правильный и выбор каждого из ответов события равновозможные? Р=1/5=0,2
7) ученик задумал однозначное натуральное число другой ученик пытается его отгадать. Какова вероятность угадать число с первой попытки? / Всего однозначных натуральных чисел 9 (1, 2, 3, ..,9), значит Р=1/9
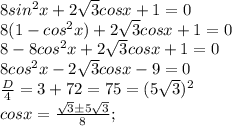
Так как функция косинус по модулю не превосходит единицы в поле действительных чисел, то выбираем 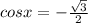
Далее решаем это уравнение:
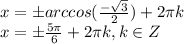
По условию нужно найти корни на промежутке ![[-\frac{7\pi}{2}; -2\pi]](/tpl/images/1359/8515/36df4.png) .
.
Это можно сделать несколькими например, с неравенства:
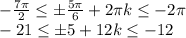
Рассмотрим случай, когда 5 имеет знак "плюс":
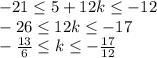
Очевидно, что из целых k подходит k = -2.
Теперь рассмотрим случай, когда 5 имеет знак "минус":
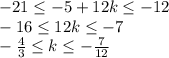
k = -1 нам подходит.
Теперь подставляем полученные k в серию корней:
1) Когда плюс - k = -2, т. е. 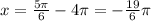
2) Когда минус - k = -1, т. е. 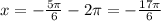
ответ: а) 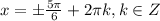
б) 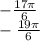
s6=b1(qⁿ-1)/(q-1)=21*((-3)⁶-1)/(-4)=-21/4*728=-3822