Для решения запишем формулу бинома Ньютона:
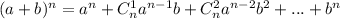
Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение 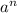 .
.
Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение 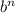 .
.
Рассмотрим многочлен 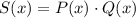 , где:
, где:
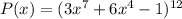
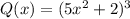
Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.
Для многочлена 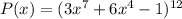 :
:
- степень определяется выражением 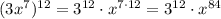 , то есть степень равна 84
, то есть степень равна 84
- свободный член равен 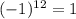
Для многочлена 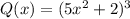 :
:
- степень определяется выражением 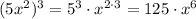 , то есть степень равна 6
, то есть степень равна 6
- свободный член равен 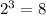
Наконец, для многочлена 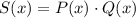 получим:
получим:
- степень определяется выражением 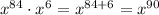 , то есть степень равна 90
, то есть степень равна 90
- свободный член равен 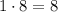
Сумма степени и свободного члена многочлена 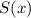 :
:
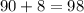
ответ: 98
b = 23
S = (a+b)/2* h = 225
См фото ====================
(a + b)/2*h = 225
(7 + 23)/2*h = 225
30/2*h = 225
15*h = 225
h = 15
Найдем боковую сторону
AB1 = (AD - BC)/2 = (23 - 7)/2 = 8
AB = √((AB1)^2 + h^2) = √(8^2 + 15^2) = √289 = 17
P = AB+BC+CD+AD = 17*2+7 + 23 = 64