ОДЗ: система: -11tgx ≥ 0
x∋ (-π/2 + πn; π/2 + πn)
Произведение равно нулю, когда хотя бы один из множителей равен нулю, а второй при этом существует.
2cos²x - cosx = 0
⇒ (2cos²x - cosx)√(-11tgx) = 0 ⇔ система:
-11tgx = 0
Решим первое уравнение системы:
2cos²x - cosx = 0 ⇔ cosx (2cosx - 1) = 0 ⇔ система: cosx = 0 ⇔ cosx = 0 ⇔
2cosx - 1 = 0 cosx = 1/2
система: x = π/2 + πn, n∋Z
x = ±π/3 + 2πn, n∋Z.
решим второе уравнение системы:
-11tgx = 0 ⇔ tgx = 0 ⇒ x = πn, n ∈Z.
x = π/2 + πn, n∋Z - не удовлетворяет ОДЗ: x∋ (-π/2 + πn; π/2 + πn) .
⇒ ответ: ±π/3 + 2πn, n∋Z.; πn, n ∈Z.
х автомашин требовалось сначала
12/х тонн груза планировалось перевозить на каждой машине
(х+2) автомашин фактически использовали
(12/(х+2) тонн груза фактически перевозила каждая машина
По условию
12/х > (12/(х+2) на 1
получаем уравнение:
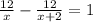
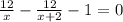
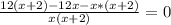
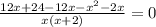
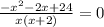
ОДЗ: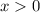 
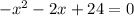
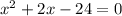
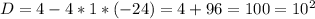
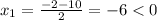не удовлетворяет ОДЗ
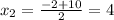
Получаем:
4 автомашины требовалось сначала
12/4 = 3 тонны груза планировалось перевозить на каждой машине
4+2 = 6 автомашин фактически использовали
ответ: 1) 4 автомашины требовалось сначала.
2) 6 автомашин фактически использовали.
3) 3 тонны груза планировалось перевозить на каждой машине.
D = 25 - (4 * 3 * (-2)) = 25 + 24 = 49,
х1 = (5 - 7) : 2,
х1 = -1.
х2 = (5 + 7) : 2,
х2 = 6.
3х^2 - 5х - 2 = (х+1)(х-6)