1. (х+4)(х+6) 2. (х -3)(х -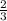 
)
Объяснение:
1. х^2 +10x - 24
a=1, b=10, c=-24
Находим дискриминант и получаем D= 4
формулы x1 =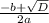 
находим первый корень, который равен -4
А с формулы х2=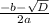
находим второй корень, который равен -6
Используем формулу квадратного трёхчлена ax^2+bx+c=a(x-x1)(x-x2)
Получаем:
x^2+10x-24= 1(x-(-4))(x-(-6)) = (x+4)(x+6)
2. 3x^2-11x+6
a=3, b=-11, c=6
Находим дискриминант и получаем D= 49
формулы x1 = 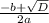находим первый корень, который равен 3
А с формулы х2=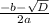 находим второй корень, который равен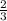
Используем формулу квадратного трёхчлена ax^2+bx+c=a(x-x1)(x-x2)
Получаем:
3x^2-11x+6= 1(x-3)(x- )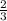
1. (х+4)(х+6) 2. (х -3)(х - )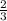
Объяснение:
1. х^2 +10x - 24
a=1, b=10, c=-24
Находим дискриминант и получаем D= 4
формулы x1 = 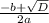находим первый корень, который равен -4
А с формулы х2=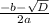 находим второй корень, который равен -6
Используем формулу квадратного трёхчлена ax^2+bx+c=a(x-x1)(x-x2)
Получаем:
x^2+10x-24= 1(x-(-4))(x-(-6)) = (x+4)(x+6)
2. 3x^2-11x+6
a=3, b=-11, c=6
Находим дискриминант и получаем D= 49
формулы x1 = 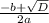находим первый корень, который равен 3
А с формулы х2=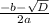 находим второй корень, который равен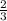
Используем формулу квадратного трёхчлена ax^2+bx+c=a(x-x1)(x-x2)
Получаем:
3x^2-11x+6= 1(x-3)(x- )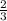
y `(x) = 2x + 4
y `(1) = 6
y (x) = 6x + b
Чтобы найти b, воспользуемся тем, что и функция и касательная имеют одно и тоже значение в точке x0 = 1.
f(1) = 7
7 = 6*1 + b
b = 1
Уравнение касательной в точке x0=1 имеет вид: y(x) = 6x + 1