Пусть х - скорость второго туриста, тогда скорость первого туриста = х + 1
время пути первого туриста = S/v = 20/(x+1)
время пути второго туриста = S/v = 20/x
известно, что первый приходит на час раньше второго, тогда:
время второго + час = время первого
20/(x + 1) + 1 = 20/x (одз: х не равно 0; х не равно - 1)
20/(х + 1) + (х + 1)/(х + 1) = 20/х
(х + 21)/(х + 1) = 20/х
20(х + 1) = х(х + 21)
20х + 20 = х² + 21х
х² + х - 20 = 0
D = 1² + 4×20 = 81 = 9²
х1 = (-1 + 9)/2 = 4 км/ч - скорость второго
х2 = (-1 - 9)/2 = -5 - не подходит по смыслу задачи
х1 + 1 = 5 км/ч - скорость первого
ответ: 4 км/ч; 5 км/ч
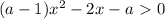
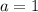, то получим линейное неравенство: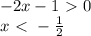
.
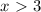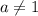- имеем квадратное неравенство.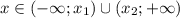 
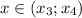
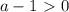, тогда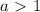 
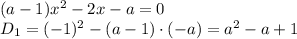
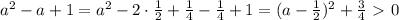
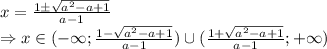
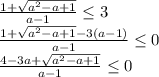
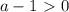, то можно перейти к следующему неравенству:![4-3a+\sqrt{a^2-a+1} \leq 0 \\\ \sqrt{a^2-a+1} \leq 3a-4 \\\ \begin{cases} a^2-a+1 \leq (3a-4)^2 \\ 3a-4\ \textgreater \ 0 \right \end{cases} \\\ \begin{cases} a^2-a+1 \leq 9a^2-24a+16 \\ 3a\ \textgreater \ 4 \right \end{cases} \\\ \begin{cases} 8a^2-23a+15 \geq 0 \\ a\ \textgreater \ \frac{4}{3} \right \end{cases} \\\ \begin{cases} a\in(-\infty;1]\cup[ \frac{15}{8} ;+\infty) \\ a\ \textgreater \ \frac{4}{3} \right \end{cases}](/tpl/images/0507/6430/22606.png)
: 
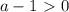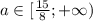
x1,2= 12+4/4=4 ; 12-4/4=2.