На рисунке прямые a и b параллельны, hello_html_m3b8c471b.gif1 = 55°. найдите hello_html_m3b8c471b.gif2. отрезки ас и bd пересекаются в их общей середине точке о. докажите, что прямые ав и cd параллельны. отрезок dm – биссектриса треугольника cde. через точку м проведена прямая, параллельная стороне cd и пересекающая сторону de в точке n. найдите углы треугольника dmn, если hello_html_m3b8c471b.gifсdе =68°. 4*. в треугольнике авс hello_html_m3b8c471b.gifа =67°, hello_html_m3b8c471b.gifс =35°, bd – биссектриса угла авс. через вершину в проведена прямая mn hello_html_m3bd0edd4.gif ac. найдите угол mbd. (указание. для каждого из возможных случаев сделайте чертеж.)

👇

Увидеть ответ

Ответ:

ольга1705

12.12.2020

решение в приложении

На рисунке прямые a и b параллельны, hello_html_m3b8c471b.gif1 = 55°. найдите hello_html_m3b8c471b.g

4,7(44 оценок)

Открыть все ответы

Ответ:

Rentels

12.12.2020

1. Найти наибольшее и наименьшее значение функции

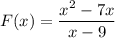$F(x)=\dfrac{x^2-7x}{x-9}$ на промежутке [-4; 1]

Точка разрыва x=9 в заданный интервал не входит.

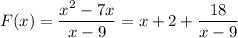
$F(x)=\dfrac{x^2-7x}{x-9}=x+2+\dfrac{18}{x-9}$

Первая производная для нахождения точек экстремумов.

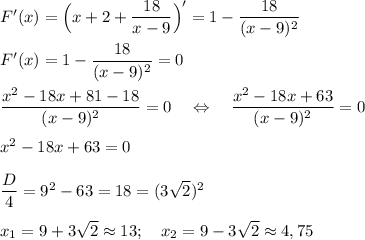
$F'(x)=\Big(x+2+\dfrac{18}{x-9}\Big)'=1-\dfrac{18}{(x-9)^2}\\\\F'(x)=1-\dfrac{18}{(x-9)^2}=0\\\\ \dfrac{x^2-18x+81-18}{(x-9)^2}=0~~~\Leftrightarrow~~~\dfrac{x^2-18x+63}{(x-9)^2}=0\\\\ x^2-18x+63=0\\\\ \dfrac{D}4=9^2-63=18=(3\sqrt2)^2\\\\x_1=9+3\sqrt2\approx 13;~~~x_2=9-3\sqrt2\approx 4,75$

Обе точки экстремумов не попадают в интервал x∈[-4; 1]

Значения функции на концах интервала

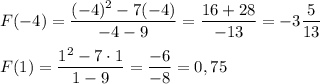
$F(-4)=\dfrac{(-4)^2-7(-4)}{-4-9}=\dfrac{16+28}{-13}=-3\dfrac{5}{13}\\\\F(1)=\dfrac{1^2-7\cdot1}{1-9}=\dfrac{-6}{-8}=0,75$

ответ: наименьшее значение функции 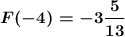$\boldsymbol{F(-4)=-3\dfrac{5}{13}}$ ;

наибольшее значение функции F(1) = 0,75

-----------------------------------------------------------------------------

2. Записать уравнение касательной к графику

функции F(x)=x⁴-2x в точке x₀=-1

Уравнение касательной имеет вид y = F(x₀) + F’(x₀)·(x - x₀)

F(-1) = x⁴-2x = (-1)⁴ - 2(-1) = 1+2 = 3

F'(-1) = (x⁴-2x)' = 4x³ - 2 = 4(-1)³ - 2 = -6

y = F(x₀) + F’(x₀)·(x - x₀) = 3 - 6 (x + 1) = 3 - 6x -6 = -6x - 3

ответ: уравнение касательной y = -6x - 3

---------------------------------------------------------------------------

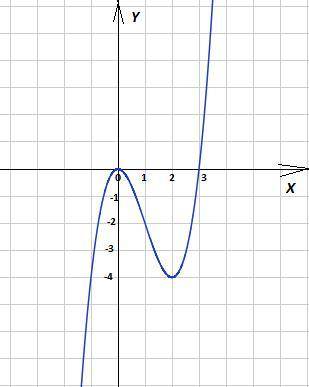
3. Исследовать функцию и построить ее график F(x)=x³-3x²

1) Область определения D(F) = R

2) Область значений E(F) = R

3) Нули функции

F(x)=x³-3x² = 0; x²(x - 3) = 0; x₁ = 0; x₂ = 3

4) Пересечение с осью OY

x = 0; F(0) = 0³-3·0² = 0

5) Экстремумы функции

F'(x) = 0; (x³-3x²)' = 0; 3x² - 6x = 0; 3x(x - 2) = 0;

x₁ = 0; F(0) = 0; F"(0) = 6x - 6 = -6 ⇒ локальный максимум.

x₂ = 2; F(2) = 2³-3·2² = -4; F"(2) = 6x - 6 = 6 ⇒ локальный минимум.

6) Монотонность функции.

Интервалы знакопостоянства первой

производной F'(x) = 3x(x - 2)

++++++++ (0) ------------- (2) +++++++++> x

/ \ /

x ∈ (-∞; 0)∪(2; +∞) - функция возрастает

x ∈ (0;2) - функция убывает

7) Функция не периодическая, общего вида (не является чётной, не является нечётной).

8) Дополнительные точки для построения

x₃ = -1; y₃ = -4; x₄ = 1; y₄ = -2

9) График функции в приложении

1. знайти найбільше і ! 1. знайти найбільше і найменше значення функції f(x)= x^2-7x/x-9 на проміжку

4,6(85 оценок)

Ответ:

alekseyovsyann

12.12.2020

1) Заметим, что, если в кучке осталось 2 спички, никому из игроков не выгодно брать из нее спичку, т.к. следующим ходом противник заберет оставшуюся спичку и победит. Тогда, если есть кучка с 1 спичкой, забираем спичку, если же есть спички числом спичек, большим 2, берем спичку из любой.

Если во всех кучках осталось по 2 спички, то было совершено 99*101=9999 ходов, а значит последнюю спичку в данный момент забрал начинающий. Тогда на 10000 ход второй вынужден забрать спичку из кучки с 2 спичками. А дальше игра оканчивается ничьей.

А значит ответ нет.

2) Заметим, что искомая сумма 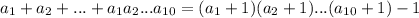$a_1+a_2+...+a_1a_2...a_{10}=(a_1+1)(a_2+1)...(a_{10}+1)-1$ .

И правда. Пусть 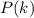P(k) - сумма всех комбинаций по 1 ... по k элементов. Тогда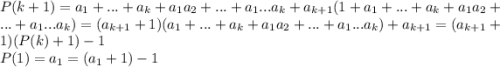 $P(k+1)=a_1+...+a_k+a_1a_2+...+a_1...a_k+a_{k+1}(1+a_1+...+a_k+a_1a_2+...+a_1...a_k)=(a_{k+1}+1)(a_1+...+a_k+a_1a_2+...+a_1...a_k)+a_{k+1}=(a_{k+1}+1)(P(k)+1)-1\\ P(1)=a_1=(a_1+1)-1$

$(a_1+1)(a_2+1)...(a_{10}+1)-1$

Т.к. числа отрицательны, то 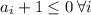$a_i+1\leq 0 \:\forall i$

Если хотя бы одно из a_i=-1 , вся сумма равна -1.

В остальных случаях 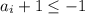$a_i+1\leq -1$ - всегда отрицательное. Но произведение 10 целых отрицательных чисел положительно, причем не меньше 1. Противоречие с тем, что $(a_1+1)(a_2+1)...(a_{10}+1)$ .