1) 3(х - 1) - 2(3 - 7х) = 2(х - 2) 2) 10(1 - 2х) = 5(2х - 3) - 3(11х - 5)
3х - 3 - 6 + 14х = 2х - 4 10 - 20х = 10х - 15 - 33х + 15
3х + 14х - 2х = - 4 + 3 + 6 - 20х - 10х + 33х = - 15 + 15 - 10
15х = 5 3х = - 10
х = 5 : 15 х = - 10 : 3
х = 5/15 = 1/3 х = - 10/3 = - 3 1/3
3) 1,3(х - 0,7) - 0,12(х + 10) - 5х = - 9,75
1,3х - 0,91 - 0,12х - 1,2 - 5х = - 9,75
1,3х - 0,12х - 5х = - 9,75 + 0,91 + 1,2
- 3,82х = - 7,64
х = - 7,64 : (- 3,82)
х = 2
4) 2,5(0,2 + х) - 0,5(х - 0,7) - 0,2х = 0,5
0,5 + 2,5х - 0,5х + 0,35 - 0,2х = 0,5
2,5х - 0,5х - 0,2х = 0,5 - 0,5 - 0,35
1,8х = - 0,35
х = - 0,35 : 1,8
х = - 35/180 = - 7/36
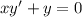
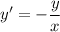 - уравнение с разделяющимися переменными
- уравнение с разделяющимися переменными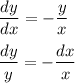
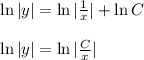
 - общее решение
- общее решение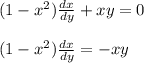

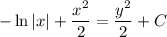 - общий интеграл
- общий интеграл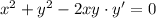

 , тогда
, тогда 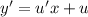



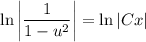
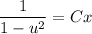
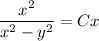 - общий интеграл
- общий интеграл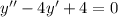
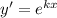 , тогда будем иметь характеристическое уравнение следующего вида:
, тогда будем иметь характеристическое уравнение следующего вида:
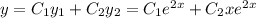 - общее решение
- общее решение
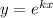 , тогда получаем
, тогда получаем
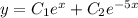

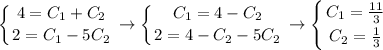
 - частное решение
- частное решение
45796 рублей .
Объяснение:
1) 40000*0,07 = 2800 (р) - проценты за первый год;
2) 40000+2800= 42800(р) - на счету через год;
3) 42800*0,07= 2996 (р) - проценты за второй год;
4) 42800+2996= 45796 (р) - на счету через два года .
Воспользуемся формулой сложных процентов :