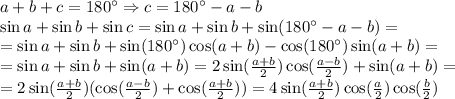
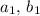 , а минимум будет иметь то же по модулю значения, но обратный знак (если есть некоторое максимальное значение при
, а минимум будет иметь то же по модулю значения, но обратный знак (если есть некоторое максимальное значение при 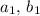 , то взяв
, то взяв 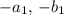 мы получим, что синус поменяет знак на противоположный, а косинусы сохранят знак. Если же у минимума модуль больше, чем у максимума, то также поменяем знак и получим новый максимум)
мы получим, что синус поменяет знак на противоположный, а косинусы сохранят знак. Если же у минимума модуль больше, чем у максимума, то также поменяем знак и получим новый максимум)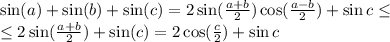
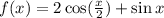 :
: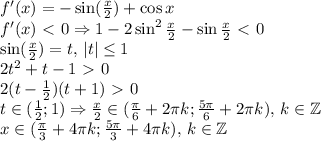
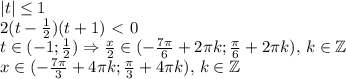
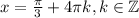
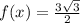
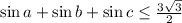
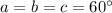 достигается это значение.
достигается это значение.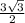
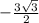
Свойства линейной функции:
1) Область определения линейной функции есть вся вещественная ось;
2) Если k ≠ 0, то область значений линейной функции есть вся вещественная ось. Если k = 0, то область значений линейной функции состоит из числа b;
3) Четность и нечетность линейной функции зависят от значений коэффициентов k и b.
a) b ≠ 0, k = 0, следовательно, y = b – четная;
b) b = 0, k ≠ 0, следовательно y = kx – нечетная;
c) b ≠ 0, k ≠ 0, следовательно y = kx + b – функция общего вида;
d) b = 0, k = 0, следовательно y = 0 – как четная, так и нечетная функция.
4) Свойством периодичности линейная функция не обладает;
5) Точки пересечения с осями координат:
D = 169 - 120 = 49 = 7^2
X1 = ( 13 + 7 ) : 12 = 5/3 = 1 2/3
X2 = ( 13 - 7 ) : 12 = 1/2
2) 6x^2 - 4x - 10 = 6( x - 1 2/3 )( x + 1 )
D = 16 + 240 = 256 = 16^2
X1 = ( 4 + 16 ) : 12 = 5/3 = 1 2/3
X2 = ( 4 - 16 ) : 12 = - 1
3) сокращаем числитель и знаменатель дроби на 6( Х - 1 2/3 ), получили ( Х - 1/2 ) / ( Х + 1 )
4) Х = - 1
( - 1 - 1/2 ) / ( - 1 + 1 ) = 0