ответ: h1=h5=5/3м = 1 2/3 м
h2=h4=8/3м= 2 2/3 м
Объяснение:
Учитывая , что OB - ось симметрии параболы , то в качестве начала координат выберет точку O . Тогда AC лежит на оси x , а OB лежит на оси y. Поскольку вершина лежит на оси y , то парабола имеет вид:
y=a*x^2 +b
Коэффициент b соответствует вершине параболы
b=OB= 3м
Длинны отрезков OA=OC=12/2=6 соответствуют положительному корню параболы :
a* 6^2+3=0
a= -3/36= -1/12
Таким образом парабола имеет вид:
y= 3 - x^2/12
Найдём высоты столбов
Нумерацию столбов будем считать слева направо.
h1=h5=y(+-4м)=3 -16/12 = 3-4/3= 5/3 м
h2=h4=y(+-2м)=3 -4/12= 3-1/3= 8/3 м
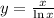
1. Область определения: На ноль делить нельзя --> 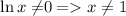 и х не отрицательный т.к. х под натуральным логарифмом. Итоге: x∈[0;1)∪(1;+∞)
и х не отрицательный т.к. х под натуральным логарифмом. Итоге: x∈[0;1)∪(1;+∞)
2. Функция общего вида т.к. f(-x)≠±f(x)
3. Точки пересечения с осями:
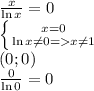 Только одна точка (0;0)
Только одна точка (0;0)
4. Исследование с 1ой производной:
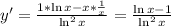
см. внизу.
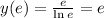
5. Исследование со 2ой производной:
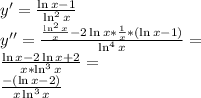
см. внизу.
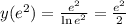
6. Асимптоты:
Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты: 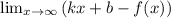
Находим коэффициент k: 
Находим коэффициент b: 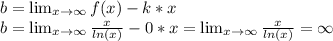
Предел равен ∞, следовательно, наклонные асимптоты функции отсутствуют.
Найдем вертикальные асимптоты. Для этого определим точки разрыва: 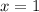
Находим переделы в точке 1: 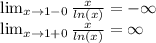
Значит точка разрыва II рода и является вертикальной асимптотой.