К натуральному числу Х справа приписали три цифры, значит, само число увеличили в 1000 раз и добавили к нему некое трёхзначное число А, получилось 1000 Х + А, которое равно сумме всех чисел от 1 до Х.
Запишем эту сумму по-разному, от меньшего к большему, и наоборот. Получатся два верных равенства, которые можно почленно сложить.
1 + 2 + 3 + ... + (Х-2) + (Х-1) + Х = 1000 Х + А
Х + (Х-1) + (Х-2) + ... + 3 + 2 + 1 = 1000 Х + А
------------------------------------------------------------------------
(Х+1)+(Х+1)+(Х+1)+ ... + (Х+1) + (Х+1) + (Х+1)=2(1000 Х + А)
Слева сумма Х одинаковых скобок (Х+1) :
(Х + 1) Х = 2000 Х + 2 А
Разделим обе части равенства на Х (по условию Х - натуральное число, поэтому Х ≠ 0)
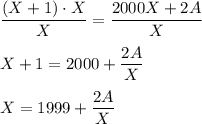
Итак, исходное число Х ≥ 1999.
По условию А - трёхзначное число, максимальное значение которого 999. Тогда 2·999=1998 < 1999. Следовательно, дробь
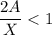для любых трёхзначных чисел А.
Из условия, что число Х - натуральное и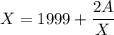 
следует, что число Х = 1999
ответ: Х = 1999
Рассмотрим события:
A - передан сигнал 0
B - передан сигнал 1
M|A - переданный сигнал 0 искажен
M|B - переданный сигнал 1 искажен
Так как сигналы типа 0 составляют 60% ото общего числа сигналов, а сигналы типа 1 - 40%, то вероятности появления этих сигналов равны:
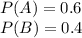
Вероятность искажения наугад взятого сигнала равна сумме попарных произведений вероятностей появления определенного сигнала на соответствующую вероятность искажения:
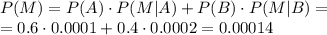
Вероятность того, что искаженный сигнал является сигналом типа 1 определим по формуле Байеса (выделим долю искаженных сигналов типа 1 из общего количества искаженных сигналов):
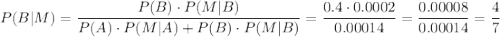
События правильной передачи сигнала и его искажения - противоположные. Вероятность того, что правильно переданный сигнал является сигналом типа 1:
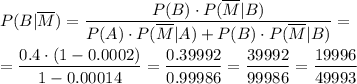
5-3+12<2х-3х
14<-х |*-1
х=14