Объяснение:
Нужно заданные формулы представить в виде комбинации из x1+x2 и x1*x2.
A) x1^2 + x2^2 = (x1+x2)^2 - 2*x1*x2
B) x1*x2^3 + x2*x1^3 = x1*x2*(x2^2 + x1^2) = x1*x2*((x1+x2)^2 - 2*x1*x2)
C) x1/x2^2 + x2/x1^2 = (x1^3 + x2^3)/(x1*x2)^2 = (x1+x2)(x1^2-x1*x2+ x2^2)/(x1*x2)^2 = (x1+x2)((x1+x2)^2 - 3*x1*x2)/(x1*x2)^2
D) x1^4 + x2^4 = (x1+x2)^4 - 4x1^2 - 6*x1*x2 - 4x2^2 = (x1+x2)^4 - 4((x1+x2)^2 - 2*x1*x2) - 6*x1*x2.
Теперь остаётся подставить данные из теоремы Виета.
x1+x2 = - b/a = - 8/3
x1*x2 = c/a = - 1/3
A) x1^2 + x2^2 = ((-8/3)^2 - 2(-1/3)) = 64/9 + 2/3 = 64/9 + 6/9 = 70/9
Остальные точно также.
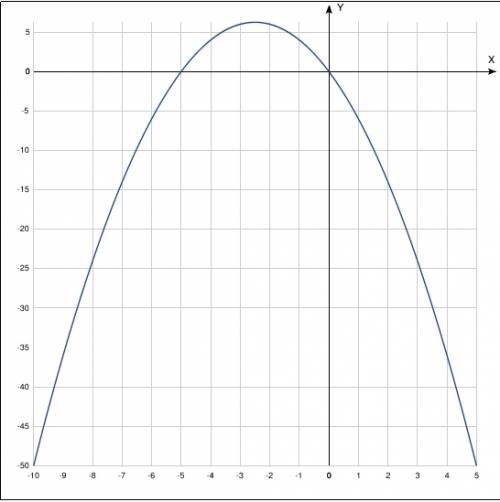
y=-x(x+5)
раскрываем скобки
y=-x²-5x
уравнение вида y=ax²+bx+c, a≠0 называется параболой
у нас a=-1, b=-5, c=0
Так как а<0, то ветви нашей параболы смотрят вниз
вершина параболы находится в точке (-b/2a; (4ac-b²)/4a), подставляем наши значения а, b и с. Получаем вершину параболы (-2,5; 6,25)
Терерь найдем точки, в которых парабола пересекается с осью Х,
-x(x+5)=0
x₁=0 и x₂=-5
То есть парабола проходит через точки (-5;0) и (0;0)
Теперь у же можно и нарисовать хоть схематично, хоть по точкам (см вложение)